
【題目】綜合與實踐:
問題情境:在一次綜合實踐活動課上,同學們以菱形為對象,研究菱形旋轉中的問題:
已知,在菱形ABCD中,BD為對角線,![]() ,AB=4,將菱形ABCD繞頂點A順時針旋轉,旋轉角為
,AB=4,將菱形ABCD繞頂點A順時針旋轉,旋轉角為![]() (單位°).旋轉后的菱形為
(單位°).旋轉后的菱形為![]() .在旋轉探究活動中提出下列問題,請你幫他們解決.
.在旋轉探究活動中提出下列問題,請你幫他們解決.
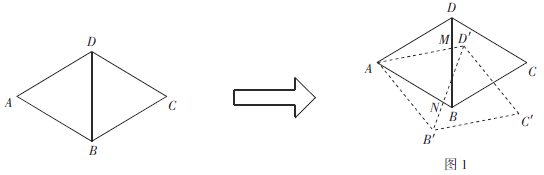
觀察證明:
(1)如圖1,若旋轉角![]() ,
,![]() 與BD相交于點M,AB與
與BD相交于點M,AB與![]() 相交于點N.請說明線段DM與
相交于點N.請說明線段DM與![]() 的數量關系;
的數量關系;
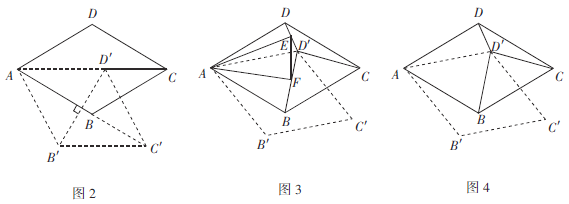
操作計算:
(2)如圖2,連接![]() ,菱形ABCD旋轉的過程中,當
,菱形ABCD旋轉的過程中,當![]() 與AB互相垂直時,
與AB互相垂直時,![]() 的長為 ;
的長為 ;
(3)如圖3,若旋轉角![]() ,分別連接
,分別連接![]() ,
,![]() ,過點A分別作
,過點A分別作![]() ,
,![]() ,連接EF,菱形ABCD旋轉的過程中,發現在
,連接EF,菱形ABCD旋轉的過程中,發現在![]() 中存在長度不變的線段EF,請求出EF長度;
中存在長度不變的線段EF,請求出EF長度;
操作探究:
(4)如圖4,在(3)的條件下,請判斷以![]() ,
,![]() ,
,![]() 三條線段長度為邊的三角形是什么特殊三角形,并說明理由.
三條線段長度為邊的三角形是什么特殊三角形,并說明理由.
【答案】(1)![]() ,理由見解析;(2)
,理由見解析;(2)![]() ;(3)2;(4)以
;(3)2;(4)以![]() ,
,![]() ,
,![]() 三條線段為邊的三角形是直角三角形,理由見解析
三條線段為邊的三角形是直角三角形,理由見解析
【解析】
(1)根據旋轉的性質利用ASA易證得![]() ,從而證得
,從而證得![]() ;
;
(2)證得點![]() 在菱形的對角線AC上,即可求解;
在菱形的對角線AC上,即可求解;
(3)利用等腰三角形三線合一的性質證明EF是![]() 的中位線,即可求解;
的中位線,即可求解;
(4)以![]() 為邊向外作等邊三角形
為邊向外作等邊三角形![]() ,利用
,利用![]() 證得
證得![]() ,求得
,求得![]() ,即可求解.
,即可求解.
(1)![]() ,
,
理由如下:
∵四邊形ABCD是菱形,
∴AB= AD.
∴∠ADB=∠ABD,
由旋轉的性質可得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,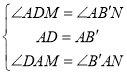 ,
,
∴![]() (ASA) ,
(ASA) ,
∴![]() ;
;
(2)連接菱形ABCD的對角線AC、BD相交于O,
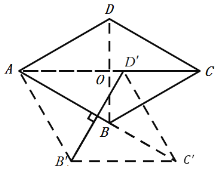
∵四邊形ABCD是菱形,且![]() ,AB=4,
,AB=4,
∴![]() ,
,
∴![]() ,則
,則![]() ,
,
根據旋轉的性質,且![]() 與AB互相垂直,
與AB互相垂直,
∴![]() ,
,
∴點![]() 在菱形ABCD的對角線AC上,
在菱形ABCD的對角線AC上,
∴![]()
∴![]() ;
;
(3)如圖,連接BD,
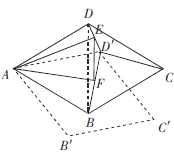
根據旋轉的性質可知:![]()
∵ AE⊥D![]() ,
,
∴![]() (等腰三角形三線合一),同理BF=F
(等腰三角形三線合一),同理BF=F![]() ,
,
∴EF是![]() 的中位線,
的中位線,
∴![]() ,
,
∵四邊形ABCD是菱形,
∴AB=AD,
又∵![]() ,
,![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∴![]() ;
;
(4)以![]() ,
,![]() ,
,![]() 三條線段為邊的三角形是直角三角形,
三條線段為邊的三角形是直角三角形,
理由如下:
如圖,以![]() 為邊向外作等邊三角形
為邊向外作等邊三角形![]() ,連接DB,CM,
,連接DB,CM,
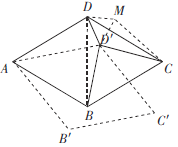
∵四邊形ABCD是菱形,![]() ,
,
∴![]() 與
與![]() 是等邊三角形,
是等邊三角形,![]() ,
,
由(3)可知:![]() 與
與![]() 都是等腰三角形,
都是等腰三角形,
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
∵![]() 與
與![]() 都是等邊三角形,
都是等邊三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
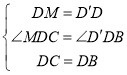 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
即以![]() ,
,![]() ,
,![]() 三條線段長度為邊的三角形是直角三角形.
三條線段長度為邊的三角形是直角三角形.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:
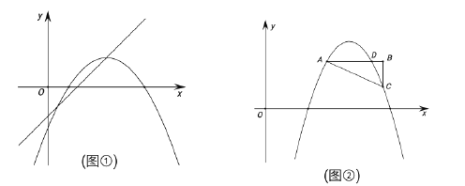
【題目】如圖①,將拋物線![]() 平移到頂點恰好落在直線
平移到頂點恰好落在直線![]() 上,并設此時拋物線頂點的橫坐標為
上,并設此時拋物線頂點的橫坐標為![]() .
.
(1)求拋物線的解析式(用含![]() 、
、![]() 的代數式表示);
的代數式表示);
(2)如圖②,![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 、
、![]() 三點,
三點,![]() ,
,![]() 軸,
軸,![]() ,
,![]() .
.
①求![]() 的面積(用含
的面積(用含![]() 的代數式表示);
的代數式表示);
②若![]() 的面積為1,當
的面積為1,當![]() 時,
時,![]() 的最大值為-3,求
的最大值為-3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學活動課上,某校初三數學老師帶領學生去測河寬,如圖所示,某學生在河東岸點![]() 處觀測到河對岸水邊有一點
處觀測到河對岸水邊有一點![]() ,測得
,測得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,沿河岸向北前行20米到達
的方向上,沿河岸向北前行20米到達![]() 處,測得
處,測得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,請你根據以上數據,幫助該同學計算出這條河的寬度.(參考數值:tan31°≈
的方向上,請你根據以上數據,幫助該同學計算出這條河的寬度.(參考數值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,動點
,動點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,點
同時出發,點![]() 以
以![]() 的速度向終點
的速度向終點![]() 勻速運動,點
勻速運動,點![]() 以
以![]() 的速度向終點
的速度向終點![]() 勻速運動,當有一點到達終點時,另一點也停止運動.設運動時間為
勻速運動,當有一點到達終點時,另一點也停止運動.設運動時間為![]() .
.

(1)當![]() 時,求四邊形
時,求四邊形![]() 的面積;
的面積;
(2)當![]() 為何值時,
為何值時,![]() 為
為![]() ?
?
(3)當![]() 為何值時,以點
為何值時,以點![]() ,
,![]() ,
,![]() 為頂點的三角形是等腰三角形?
為頂點的三角形是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列一組方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通過觀察,發現了其中蘊含的規律,并順利地求出了前三個方程的解第①個方程的解為
,…小明通過觀察,發現了其中蘊含的規律,并順利地求出了前三個方程的解第①個方程的解為![]() ;第②個方程的解為
;第②個方程的解為![]() ;第③個方程的解為
;第③個方程的解為![]() .若n為正整數,且關于x的方程
.若n為正整數,且關于x的方程![]() 的一個解是
的一個解是![]() ,則n的值等于____________.
,則n的值等于____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解
如圖1,![]() 中,沿
中,沿![]() 的平分線
的平分線![]() 折疊,剪掉重疊部分;將余下部分沿
折疊,剪掉重疊部分;將余下部分沿![]() 的平分線
的平分線![]() 折疊,剪掉重疊部分;……;將余下部分沿
折疊,剪掉重疊部分;……;將余下部分沿![]() 的平分線
的平分線![]() 折疊,點
折疊,點![]() 與點
與點![]() 重合,無論折疊多少次,只要最后一次恰好重合,我們就稱
重合,無論折疊多少次,只要最后一次恰好重合,我們就稱![]() 是
是![]() 的好角.
的好角.
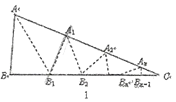
情形一:如圖2,沿等腰三角形![]() 頂角
頂角![]() 的平分線
的平分線![]() 折疊,點
折疊,點![]() 與點
與點![]() 重合;
重合;
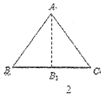
情形二:如圖3,沿![]() 的
的![]() 的平分線
的平分線![]() 折疊,剪掉重疊部分;將余下的部分沿
折疊,剪掉重疊部分;將余下的部分沿![]() 的平分線
的平分線![]() 折疊,此時點
折疊,此時點![]() 與點
與點![]() 重合.
重合.
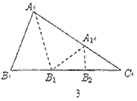
探究發現
(1)![]() 中,
中,![]() ,經過兩次折疊,問
,經過兩次折疊,問![]()
![]() 的好角(填寫“是”或“不是”);
的好角(填寫“是”或“不是”);
(2)若經過三次折疊發現![]() 是
是![]() 的好角,請探究
的好角,請探究![]() 與
與![]() (假設
(假設![]() )之間的等量關系 ;
)之間的等量關系 ;
根據以上內容猜想:若經過![]() 次折疊
次折疊![]() 是
是![]() 的好角,則
的好角,則![]() 與
與![]() (假設
(假設![]() )之間的等量關系為 ;
)之間的等量關系為 ;
應用提升:
(3)小麗找到一個三角形,三個角分別為![]() ,
,![]() ,
,![]() ,發現 是此三角形的好角;
,發現 是此三角形的好角;
(4)如果一個三角形的最小角是![]() ,且滿足該三角形的三個角均是此三角形的好角;
,且滿足該三角形的三個角均是此三角形的好角;
則此三角形另外兩個角的度數 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在同一平面內,將△ABC繞A點逆時針旋轉到△ADE的位置.若AC⊥DE,∠ABD=62°,則∠ACB的度數為( )

A.56°B.44°C.34°D.40°
查看答案和解析>>
科目:初中數學 來源: 題型:
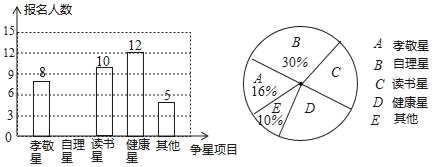
【題目】某小學開展寒假爭星活動,學生可以從“自理星”、“讀書星”、“健康星”、“孝敬星”等中選一個項目參加爭星競選,根據該校一年級某班學生的“爭星”報名情況,繪制成了如下兩幅不完整的統計圖,請根據圖中信息回答下列問題:
(1)參加調查的學生共有 人.
(2)將條形統計圖補充完整;
(3)請計算扇形統計圖中“讀書星”對應的扇形圓心角度數;
(4)根據調查結果,試估計該小學全校3600名學生中爭當“健康星”的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com