【題目】如圖，在菱形ABCD中，過點D作DE⊥AB于點E，作DF⊥BC于點F，連接EF．求證：（1）△ADE≌△CDF；（2）∠BEF=∠BFE．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】在矩形ABCD中，AB=4，AD=3，現將紙片折疊，點D的對應點記為點P，折痕為EF(點E、F是折痕與矩形的邊的交點)，再將紙片還原．
（1）若點P落在矩形ABCD的邊AB上(如圖1)．
①當點P與點A重合時，∠DEF= °，當點E與點A重合時，∠DEF= °．
②當點E在AB上時，點F在DC上時(如圖2)，若AP=
，求四邊形EPFD的周長．
（2）若點F與點C重合，點E在AD上，線段BA與線段FP交于點M(如圖3)，當AM=DE時，請求出線段AE的長度．
（3）若點P落在矩形的內部(如圖4)，且點E、F分別在AD、DC邊上，請直接寫出AP的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】珠海市水務局對某小區居民生活用水情況進行了調査．隨機抽取部分家庭進行統計，繪制成如下尚未完成的頻數分布表和頻率分布直方圖．請根據圖表，解答下列問題：
月均用水量（單位：噸 | 頻數 | 頻率 |
2≤x＜3 | 4 | 0.08 |
3≤x＜4 | a | b |
4≤x＜5 | 14 | 0.28 |
5≤x＜6 | 9 | c |
6≤x＜7 | 6 | 0.12 |
7≤x＜8 | 5 | 0.1 |
合計 | d | 1.00 |
（1）b= ，c= ，并補全頻數分布直方圖；
（2）為鼓勵節約用水用水，現要確定一個用水量標準P（單位：噸），超過這個標準的部分按1.5倍的價格收費，若要使60%的家庭水費支出不受影響，則這個用水量標準P= 噸；
（3）根據該樣本，請估計該小區400戶家庭中月均用水量不少于5噸的家庭約有多少戶？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知:正方形ABCD，等腰直角三角板的直角頂點落在正方形的頂點D處，使三角板繞點D旋轉.
(1)當三角板旋轉到圖1的位置時，猜想CE與AF的數量關系，并加以證明；
(2)在(1)的條件下，若DE:AE:CE= 1: 
:3，求∠AED的度數；
(3)若BC= 4，點M是邊AB的中點，連結DM，DM與AC交于點O，當三角板的一邊DF與邊DM重合時(如圖2)，若OF=
，求CN的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】平面直角坐標系中，直線l1:
與x軸交于點A，與y軸交于點B，直線l2:
與x軸交于點C，與直線l1交于點P．
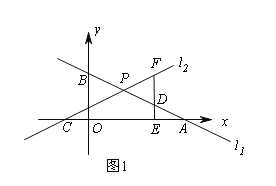
（1）當k=1時，求點P的坐標；
（2）如圖1，點D為PA的中點，過點D作DE⊥x軸于E，交直線l2于點F，若DF=2DE，求k的值；
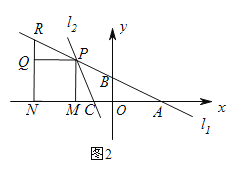
（3）如圖2，點P在第二象限內，PM⊥x軸于M，以PM為邊向左作正方形PMNQ，NQ的延長線交直線l1于點R，若PR=PC，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們給出如下定義：順次連接任意一個四邊形各邊中點所得的四邊形叫中點四邊形．
（1）如圖1，四邊形ABCD中，點E，F，G，H分別為邊AB，BC，CD，DA的中點．求證：中點四邊形EFGH是平行四邊形；
（2）如圖2，點P是四邊形ABCD內一點，且滿足PA=PB，PC=PD，∠APB=∠CPD，點E，F，G，H分別為邊AB，BC，CD，DA的中點，猜想中點四邊形EFGH的形狀，并證明你的猜想；
（3）若改變（2）中的條件，使∠APB=∠CPD=90°，其他條件不變，直接寫出中點四邊形EFGH的形狀．（不必證明）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】彈簧掛上物體后會伸長，（在彈性限度
內）已知一彈簧的長度
與所掛物體的質量
之間的關系如下表：
物體的質量 | 0 | 1 | 2 | 3 | 4 | 5 |
彈簧的長度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
（1）當物體的質量為
時，彈簧的長度是多少？
（2）如果物體的質量為
，彈簧的長度為
，根據上表寫出
與x的關系式；
（3）當物體的質量為
時，求彈簧的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道，任意一個正整數
都可以進行這樣的分解：
（
是正整數，且
），在的所有這種分解中，如果兩因數之差的絕對值最小，我們就稱
是的最佳分解，產規定：
，例如：12可以分解成
，
，
，因為
，所以是12的最佳分解，所以
.
（1）求
；
（2）若正整數
是4的倍數，我們稱正整數為“四季數”，如果一個兩位正整數
，
（
，
為自然數），交換個位上的數字與十位上的數字得到的新兩位正整數減去原來的兩位正整數所得的差為“四季數”，那么我們稱這個數為“有緣數”，求所有“有緣數”中
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
