
【題目】已知:如圖,AD是△ABC的中線,E為AD的中點(diǎn),過(guò)點(diǎn)A作AF∥BC交BE延長(zhǎng)線于點(diǎn)F,連接CF.
(1)如圖1,求證:四邊形ADCF是平行四邊形;
(2)如圖2,連接CE,在不添加任何輔助線的情況下,請(qǐng)直接寫(xiě)出圖2中所有與△BDE面積相等的三角形.

【答案】(1)證明見(jiàn)解析;(2)△AEF、 △ABE、 △ACE 、△CDE.
【解析】
(1)證明△AEF≌△DEB,可得AF=DB,再根據(jù) BD=CD可得AF=CD,再由AF//CD,根據(jù)有一組對(duì)邊平行且相等的四邊形是平行四邊形即可證得結(jié)論;
(2)根據(jù)三角形中線將三角形分成面積相等的兩個(gè)三角形以及全等三角形的面積相等即可得.
(1)![]() D為BC的點(diǎn)、E為AD的中點(diǎn)
D為BC的點(diǎn)、E為AD的中點(diǎn)
![]() BD=CD、AE=DE
BD=CD、AE=DE
![]() AF∥BC,
AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中
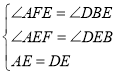 ,
,
∴△AEF≌△DEB,
∴AF=DB,
又∵ BD=CD
∴AF=CD,
又![]() AF∥BC,
AF∥BC,
∴四邊形ADCF是平行四邊形;
(2)∵△AEF≌△DEB,
∴S△AEF=S△DEB,
∵D為BC中點(diǎn),
∴S△CDE=S△DEB,
∵E為AD中點(diǎn),
∴S△ABE=S△DEB,S△ACE= S△CDE=S△DEB,
綜上,與△BDE面積相等的三角形有△AEF、 △ABE、 △ACE 、△CDE.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形網(wǎng)格中的每個(gè)小正方形的邊長(zhǎng)都是1,每個(gè)小格的頂點(diǎn)叫格點(diǎn),網(wǎng)格中有以格點(diǎn)A、B、C為頂點(diǎn)的△ABC,請(qǐng)你根據(jù)所學(xué)的知識(shí)回答下列問(wèn)題:

(1)求△ABC的面積;(2)判斷△ABC的形狀,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
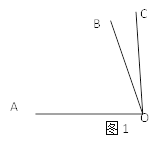
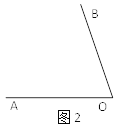
【題目】課堂上,老師在黑板上出了一道題:在同一平面內(nèi),若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度數(shù).
下面是七年級(jí)同學(xué)小明在黑板上寫(xiě)的解題過(guò)程:
解:根據(jù)題意可畫(huà)出圖(如圖1)
因?yàn)椤?/span>AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同學(xué)們?cè)谙旅孀h論,都說(shuō)小明解答不全面,還有另一種情況.請(qǐng)按下列要求完成這道題的求解.
(1)依照?qǐng)D1,用尺規(guī)作圖的方法將另一種解法的圖形在圖2中補(bǔ)充完整.
(2)結(jié)合第(1)小題的圖形寫(xiě)出求∠AOC的度數(shù)的完整過(guò)程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
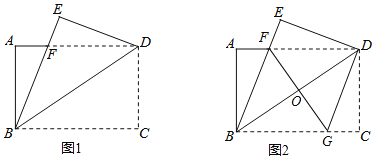
【題目】如圖1,將一張矩形紙片ABCD沿著對(duì)角線BD向上折疊,頂點(diǎn)C落到點(diǎn)E處,BE交AD于點(diǎn)F.
(1)求證:△BDF是等腰三角形;
(2)如圖2,過(guò)點(diǎn)D作DG∥BE,交BC于點(diǎn)G,連接FG交BD于點(diǎn)O.
①判斷四邊形BFDG的形狀,并說(shuō)明理由;
②若AB=6,AD=8,求FG的長(zhǎng)為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,折線ABCDE描述了一汽車(chē)在某一直路上行駛時(shí)汽車(chē)離出發(fā)地的距離s(千米)和行駛時(shí)間t(小時(shí))間的變量關(guān)系,則下列結(jié)論正確的是( )
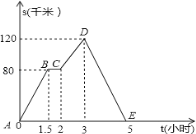
A. 汽車(chē)共行駛了120千米
B. 汽車(chē)在行駛途中停留了2小時(shí)
C. 汽車(chē)在整個(gè)行駛過(guò)程中的平均速度為每小時(shí)24千米
D. 汽車(chē)自出發(fā)后3小時(shí)至5小時(shí)間行駛的速度為每小時(shí)60千米
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市居民用水實(shí)行階梯水價(jià),實(shí)施細(xì)則如下表:
分檔水量 | 年用水量 (立方米) | 水價(jià) (元/立方米) |
第一階梯 | 0~180(含) | 5.00 |
第二階梯 | 181~260(含) | 7.00 |
第三階梯 | 260以上 | 9.00 |
例如,某戶家庭年使用自來(lái)水200 m3,應(yīng)繳納:180×5+(200-180)×7=1040元;
某戶家庭年使用自來(lái)水300 m3,應(yīng)繳納:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小剛家2017年共使用自來(lái)水170 m3,應(yīng)繳納 元;小剛家2018年共使用自來(lái)水260 m3,應(yīng)繳納 元.
(2)小強(qiáng)家2018年使用自來(lái)水共繳納1180元,他家2018年共使用了多少自來(lái)水?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中正確的是( )
A. 若|a|=﹣a,則 a 一 定是負(fù)數(shù)
B. 單項(xiàng)式 x3y2z 的系數(shù)為 1,次數(shù)是 6
C. 若 AP=BP,則點(diǎn) P 是線段 AB 的中點(diǎn)
D. 若∠AOC=![]() ∠AOB,則射線 OC 是∠AOB 的平分線
∠AOB,則射線 OC 是∠AOB 的平分線
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
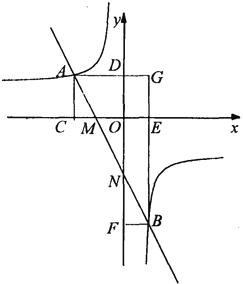
【題目】直線MN與x軸、y軸分別交于點(diǎn)M、N,并且經(jīng)過(guò)第二、三、四象限,與反比例函數(shù)y=![]() (k<0)的圖象交于點(diǎn)A、B,過(guò)A、B兩點(diǎn)分別向x軸、y軸作垂線,垂足為C、D、E、F,AD與BF交于G點(diǎn).
(k<0)的圖象交于點(diǎn)A、B,過(guò)A、B兩點(diǎn)分別向x軸、y軸作垂線,垂足為C、D、E、F,AD與BF交于G點(diǎn).
(1)比較大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求證:①AGGE=BFBG;
②AM=BN;
(3)若直線AB的解析式為y=﹣2x﹣2,且AB=3MN,則k的值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某日的錢(qián)塘江觀潮信息如圖:

按上述信息,小紅將“交叉潮”形成后潮頭與乙地之間的距離s(千米)與時(shí)間t(分鐘)的函數(shù)關(guān)系用圖3表示,其中:“11:40時(shí)甲地‘交叉潮’的潮頭離乙地12千米”記為點(diǎn)A(0,12),點(diǎn)B坐標(biāo)為(m,0),曲線BC可用二次函數(shù)s=![]() t2+bt+c(b,c是常數(shù))刻畫(huà).
t2+bt+c(b,c是常數(shù))刻畫(huà).
(1)求m的值,并求出潮頭從甲地到乙地的速度;
(2)11:59時(shí),小紅騎單車(chē)從乙地出發(fā),沿江邊公路以0.48千米/分的速度往甲地方向去看潮,問(wèn)她幾分鐘后與潮頭相遇?
(3)相遇后,小紅立即調(diào)轉(zhuǎn)車(chē)頭,沿江邊公路按潮頭速度與潮頭并行,但潮頭過(guò)乙地后均勻加速,而單車(chē)最高速度為0.48千米/分,小紅逐漸落后.問(wèn)小紅與潮頭相遇到落后潮頭1.8千米共需多長(zhǎng)時(shí)間?(潮水加速階段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com