
【題目】如圖,已知拋物線經過A(﹣2,0),B(﹣3,3)及原點O,頂點為C.
(1)求拋物線的函數解析式.
(2)設點D在拋物線上,點E在拋物線的對稱軸上,若四邊形AODE是平行四邊形,求點D的坐標.
(3)聯接BC交x軸于點F.y軸上是否存在點P,使得△POC與△BOF相似?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】
(1)解:設拋物線的解析式為y=ax2+bx+c(a≠0),
將點A(﹣2,0),B(﹣3,3),O(0,0),代入可得:  ,
,
解得: ![]() ,
,
故拋物線函數解析式為:y=x2+2x

(2)解:∵AO為平行四邊形的一邊,
∴DE∥AO,DE=AO,
∵A(﹣2,0),
∴DE=AO=2,
∵四邊形AODE是平行四邊形,
D在對稱軸x=﹣1的右側,D點橫坐標為:﹣1+2=1,帶入拋物線解析式得y=3,
∴D的坐標為(1,3)
(3)解:在y軸上存在點P,使得△POC與△BOF相似,理由如下:
由y=x2+2x,頂點C的坐標為(﹣1,1),
∵tan∠BOF= ![]() =1,
=1,
∴∠BOF=45°,
當點P在y軸的負半軸時,tan∠COP= ![]() =1,
=1,
∴∠COP=45°,
∴∠BOF=∠COP,
設BC的解析式為y=kx+b(k≠0),
∵圖象經過B(﹣3,3),C(﹣1,﹣1)
∴ ![]() ,
,
∴ ![]() ,
,
∴y=﹣2x﹣3;
令y=0,則x=﹣1.5.
∴F(﹣1.5,0),
∴OB=3 ![]() ,OF=1.5,OC=
,OF=1.5,OC= ![]() ,
,
①當△POC∽△FOB時,
則 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴OP= ![]() ,
,
∴P(0,﹣ ![]() );
);
②當△POC∽△BOF時,
∴ ![]() =
= ![]() ,
,
∴OP=4,
∴P(0,﹣4),
∴當△POC與△BOF相似時,點P的坐標為(0,﹣ ![]() )或(0,﹣4).
)或(0,﹣4).
【解析】(1)主要考察拋物線的解析式,只需將已知點代入y=ax2+bx+c(a≠0),即可解出a、b、c帶入原式得到拋物線的解析式。
(2)把拋物線和平行四邊形結合起來考察,利用平行四邊形的特征找到于AO平行且相等的線段,且兩端點分別在拋物線和拋物線的對稱軸上,由對稱軸得出橫坐標,代入拋物線方程解出D點坐標,解題思路主要是平行四邊形性質結合拋物線方程。
(3)相似三角形對應邊的比值相等,解題思路利用拋物線解出過點AB的方程,根據直線方程得到F坐標,三角形要相似,對應邊的比值要相等,從而找到P點坐標,此題主要考察三角形相似的性質,直線方程與拋物線結合,還用到解直角三角形。整個大題最容易被扣分的就是有多種情況,容易做漏,所以我們在考慮時應該假設多種情況一一排除。


科目:初中數學 來源: 題型:
【題目】甲、乙兩人以各自的交通工具、相同路線,前往距離單位10km的培訓中心參加學習.圖中l甲、l乙分別表示甲、乙前往目的地所走的路程S(km)隨時間t(分)變化的函數圖象.以下說法:①乙比甲提前12分鐘到達;②乙走了8km后遇到甲;③乙出發6分鐘后追上甲;④甲走了28分鐘時,甲乙相距3km.其中正確的是( )

A. 只有① B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求點A,B的坐標;
(2)如圖,點C為x軸正半軸上一點,且OC=OA,點D為OC的中點,連AC,AD,請探索AD+CD與![]() AC之間的大小關系,并說明理由;
AC之間的大小關系,并說明理由;

(3)如圖,過點A作AE⊥y軸于E,F為x軸負半軸上一動點( 不與(-3,0)重合 ),G在EF延長線上,以EG為一邊作∠GEN=45°,過A作AM⊥x軸,交EN于點M,連FM,當點F在x軸負半軸上移動時,式子![]() 的值是否發生變化?若變化,求出變化的范圍;若不變化,請求出其值并說明理由.
的值是否發生變化?若變化,求出變化的范圍;若不變化,請求出其值并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解本校中考體育備考情況,隨機抽去九年級部分學生進行了一次測試(滿分60分,成績均記為整數分)并按測試成績(單位:分)分成四類:A類(54≤a≤60),B類(48≤a≤53),C類(36≤a≤47),D類(a≤35)繪制出如下兩幅不完整的統計圖,請根據圖中信息,解答下列問題:
(1)請補全統計圖;
(2)在扇形統計圖匯總,表示成績類別為“C”的扇形所對應的圓心角是度;
(3)該校準備召開體育考經驗交流會,已知A類學生中有4人滿分(男生女生各有2人),現計劃從這4人中隨機選出2名學生進行經驗介紹,請用樹狀圖或列表法求所抽到的2,名學生恰好是一男一女的概率
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了創建書香校園,今年又購進一批圖書,經了解,科普書的單價比文學書的單價多4元,用1200元購進的科普書與用800元購進的文學書本數相等.
(1)今年購進的文學書和科普書的單價各是多少元?
(2)該校購買這兩種書共180本,總費用不超過2000元,且購買文學書的數量不多于42本,應選擇哪種購買方案可使總費用最低?最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
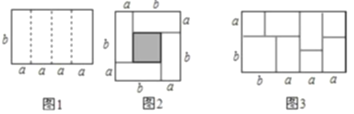
【題目】如圖是一個長為![]() 、寬為
、寬為![]() 的長方形,沿中虛線用剪刀平均分成四塊小長方形,然后用四塊小長方形拼成的一個“回形”正方形(如圖).
的長方形,沿中虛線用剪刀平均分成四塊小長方形,然后用四塊小長方形拼成的一個“回形”正方形(如圖).
(1)如圖中的陰影部分面積為: ;(用![]() 、
、![]() 的代數式表示)
的代數式表示)
(2)觀察如圖,請你寫出![]() 、
、![]() 、
、![]() 之間的等量關系是 ;
之間的等量關系是 ;
(3)根據(2)中的結論,若![]() ,
,![]() ,則
,則![]() ;
;
(4)實際上通過計算圖形的陰影可以探求相應的等式,如圖,請你寫出這個等式 ;
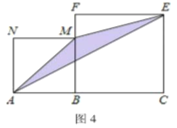
(5)如圖,線段![]() (其中
(其中![]() 為正數),點
為正數),點![]() 線在段
線在段![]() 上,在線段
上,在線段![]() 同側作正方形
同側作正方形![]() 及正方形
及正方形![]() ,連接
,連接![]() ,
,![]() ,
,![]() 得到
得到![]() .當
.當![]() 時,
時,![]() 的面積記為
的面積記為![]() ;當
;當![]() 時,
時,![]() 的面積記為
的面積記為![]() ;當
;當![]() 時,
時,![]() 的面積記為
的面積記為![]() ;當
;當![]() 時,
時,![]() 的面積記為
的面積記為![]() ,則
,則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象l與坐標軸分別交于點E,F,與雙曲線y=﹣ ![]() (x<0)交于點P(﹣1,n),且F是PE的中點,直線x=a與l交于點A,與雙曲線交于點B(不同于A),PA=PB,則a= .
(x<0)交于點P(﹣1,n),且F是PE的中點,直線x=a與l交于點A,與雙曲線交于點B(不同于A),PA=PB,則a= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,點A,B,C均在格點上.
(1)請值接寫出點A,B,C的坐標.
(2)若平移線段AB,使B移動到C的位置,請在圖中畫出A移動后的位置D,依次連接B,C,D,A,并求出四邊形ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() ,甲、乙兩人從兩地出發相向而行,甲先出發。圖中
,甲、乙兩人從兩地出發相向而行,甲先出發。圖中![]() 表示兩人離
表示兩人離![]() 地的距離
地的距離![]() 與時間
與時間![]() 的關系,結合圖象回答下列問題:
的關系,結合圖象回答下列問題:
(1)表示甲離![]() 地的距離與時間關系的圖象是_____(填
地的距離與時間關系的圖象是_____(填![]() 或
或![]() ),甲的速度是__________
),甲的速度是__________![]() ,乙的速度是____________
,乙的速度是____________![]() 。
。
(2)甲出發后多少時間兩人恰好相距![]() ?
?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com