Question

【題目】綜合與探究：

如圖1，拋物線y=﹣x2+x+與x軸分別交于A、B兩點（點A在點B的左側），與y軸交于C點．經過點A的直線l與y軸交于點D（0，﹣）．

（1）求A、B兩點的坐標及直線l的表達式；

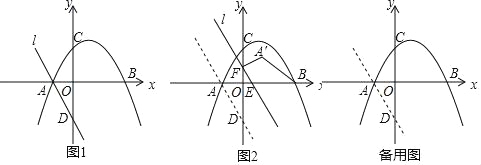
（2）如圖2，直線l從圖中的位置出發，以每秒1個單位的速度沿x軸的正方向運動，運動中直線l與x軸交于點E，與y軸交于點F，點A 關于直線l的對稱點為A′，連接FA′、BA′，設直線l的運動時間為t（t＞0）秒．探究下列問題：

①請直接寫出A′的坐標（用含字母t的式子表示）；

②當點A′落在拋物線上時，求直線l的運動時間t的值，判斷此時四邊形A′BEF的形狀，并說明理由；

（3）在（2）的條件下，探究：在直線l的運動過程中，坐標平面內是否存在點P，使得以P，A′，B，E為頂點的四邊形為矩形？若存在，請直接寫出點P的坐標； 若不存在，請說明理由．

Answer 1

【答案】（1）y=﹣x﹣；（2）見解析（3）存在

【解析】

（1）通過解方程﹣x2+x+＝0得A（1，0），B（3，0），然后利用待定系數法確定直線l的解析式；

（2）①作A′H⊥x軸于H，如圖2，利用OA＝1，OD＝得到∠OAD＝60°，再利用平移和對稱的性質得到EA＝EA′＝t，∠A′EF＝∠AEF＝60°，然后根據含30度的直角三角形三邊的關系表示出A′H，EH即可得到A′的坐標；

②把A′（t1，t）代入y＝x2＋x＋得（t1）2＋（t1）＋＝t，解方程得到t＝2，此時A′點的坐標為（2，），E（1，0），然后通過計算得到AF＝BE＝2，A′F∥BE，從而判斷四邊形A′BEF為平行四邊形，然后加上EF＝BE可判定四邊形A′BEF為菱形；

（3）討論：當A′B⊥BE時，四邊形A′BEP為矩形，利用點A′和點B的橫坐標相同得到t1＝3，解方程求出t得到A′（3，），再利用矩形的性質可寫出對應的P點坐標；當A′B⊥EA′，如圖4，四邊形A′BPE為矩形，作A′Q⊥x軸于Q，先確定此時A′點的坐標，然后利用點的平移確定對應P點坐標．

（1）當y=0時，﹣x2+x+=0，解得x1=﹣1，x2=3，則A（﹣1，0），B（3，0），

設直線l的解析式為y=kx+b，

把A（﹣1，0），D（0，﹣）代入得，解得，

∴直線l的解析式為y=﹣x﹣；

（2）①作A′H⊥x軸于H，如圖，

∵OA=1，OD=，

∴∠OAD=60°，

∵EF∥AD，

∴∠AEF=60°，

∵點A 關于直線l的對稱點為A′，

∴EA=EA′=t，∠A′EF=∠AEF=60°，

在Rt△A′EH中，EH=EA′=t，A′H=EH=t，

∴OH=OE+EH=t﹣1+t=t﹣1，

∴A′（t﹣1， t）；

②把A′（t﹣1， t）代入y=﹣x2+x+得﹣（t﹣1）2+（t﹣1）+=t，

解得t1=0（舍去），t2=2，

∴當點A′落在拋物線上時，直線l的運動時間t的值為2；

此時四邊形A′BEF為菱形，理由如下：

當t=2時，A′點的坐標為（2，），E（1，0），

∵∠OEF=60°

∴OF=OE=，EF=2OE=2，

∴F（0，），

∴A′F∥x軸，

∵A′F=BE=2，A′F∥BE，

∴四邊形A′BEF為平行四邊形，

而EF=BE=2，

∴四邊形A′BEF為菱形；

（3）存在，如圖：

當A′B⊥BE時，四邊形A′BEP為矩形，則t﹣1=3，解得t=，則A′（3，），

∵OE=t﹣1=，

∴此時P點坐標為（，）；

當A′B⊥EA′，如圖，四邊形A′BPE為矩形，作A′Q⊥x軸于Q，

∵∠AEA′=120°，

∴∠A′EB=60°，

∴∠EBA′=30°

∴BQ=A′Q=t=t，

∴t﹣1+t=3，解得t=，

此時A′（1，），E（，0），

點A′向左平移個單位，向下平移個單位得到點E，則點B（3，0）向左平移個單位，向下平移個單位得到點P，則P（，﹣），

綜上所述，滿足條件的P點坐標為（，）或（，﹣）．