
【題目】已知△ABC的三邊a,b,c,滿足a+b2+|c﹣6|+28=4![]() +10b,則△ABC的外接圓半徑=__________.
+10b,則△ABC的外接圓半徑=__________.
 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知AB∥CD,解決下列問(wèn)題:

(1)如圖①,寫出∠ABE、∠CDE和∠E之間的數(shù)量關(guān)系: ;
(2)如圖②,BP、DP分別平分∠ABE、∠CDE,若∠E=100°,求∠P的度數(shù);
(3)如圖③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,試寫出∠P與∠E的數(shù)量關(guān)系,并說(shuō)明理由.
∠CDE,試寫出∠P與∠E的數(shù)量關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
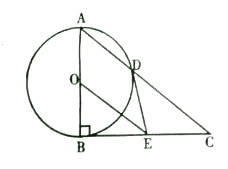
【題目】如圖,以![]() 的直角邊
的直角邊![]() 為直徑作
為直徑作![]() 交斜邊
交斜邊![]() 于點(diǎn)
于點(diǎn)![]() ,過(guò)圓心
,過(guò)圓心![]() 作
作![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .
.
(1)判斷![]() 與
與![]() 的位置關(guān)系并說(shuō)明理由;
的位置關(guān)系并說(shuō)明理由;
(2)求證:![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,△ABC的頂點(diǎn)A在第一象限,點(diǎn)B,C的坐標(biāo)分別為(2,1),(6,1),∠BAC=90°,AB=AC,直線AB交y軸于點(diǎn)P,若△ABC與△A′B′C′關(guān)于點(diǎn)P成中心對(duì)稱,則點(diǎn)A′的坐標(biāo)為( )

A. (﹣4,﹣5) B. (﹣5,﹣4) C. (﹣3,﹣4) D. (﹣4,﹣3)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某水果零售商店分兩批次從批發(fā)市場(chǎng)共購(gòu)進(jìn)“紅富士”蘋果100箱,已知第一、二次進(jìn)貨價(jià)分別為每箱50元、40元,且第二次比第一次多付款400元.
(1)求第一、二次分別購(gòu)進(jìn)“紅富士”蘋果各多少箱?
(2)商店對(duì)這100箱“紅富士”蘋果先按每箱60元銷售了75箱后出現(xiàn)滯銷,于是決定其余的每箱靠打折銷售完.要使商店銷售完全部“紅富士”蘋果所獲得的利潤(rùn)不低于1300元,問(wèn)其余的每箱至少應(yīng)打幾折銷售?(注:按整箱出售,利潤(rùn)=銷售總收人﹣進(jìn)貨總成本)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
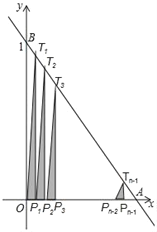
【題目】如圖,直線y=﹣x+1與兩坐標(biāo)軸分別交于A,B兩點(diǎn),將線段OA分成n等份,分點(diǎn)分別為P1,P2,P3,…,Pn﹣1,過(guò)每個(gè)分點(diǎn)作x軸的垂線分別交直線AB于點(diǎn)T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分別表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面積,則S1+S2+S3+…+Sn﹣1=__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,圖①是一個(gè)長(zhǎng)為2m,寬為2n的長(zhǎng)方形.沿圖中虛線把它分割成四塊完全相同的小長(zhǎng)方形,然后按圖②的形狀拼成一個(gè)正方形.
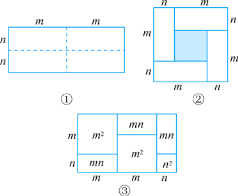
(1)求圖②中陰影部分的面積.
(2)觀察圖②,發(fā)現(xiàn)三個(gè)代數(shù)式(m+n)2,(m-n)2,mn之間的等量關(guān)系是 .
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)觀察圖③,你能得到怎樣的代數(shù)恒等式?
(5)試畫出一個(gè)幾何圖形,使它的面積能表示代數(shù)恒等式(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知AM∥CN,點(diǎn)B為平面內(nèi)一點(diǎn),AB⊥BC于B
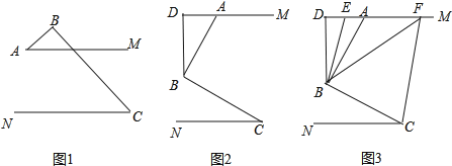
(1)如圖1,直接寫出∠A和∠C之間的數(shù)量關(guān)系;
(2)如圖2,過(guò)點(diǎn)B作BD⊥AM于點(diǎn)D,求證:∠ABD=∠C;
(3)如圖3,在(2)問(wèn)的條件下,點(diǎn)E.F在DM上,連接BE.BF.CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠ABF=2∠ABE,求∠EBC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知雙曲線y1=![]() 與直線y2=ax+b交于點(diǎn)A(﹣4,1)和點(diǎn)B(m,﹣4).
與直線y2=ax+b交于點(diǎn)A(﹣4,1)和點(diǎn)B(m,﹣4).
(1)求雙曲線和直線的解析式;
(2)直接寫出線段AB的長(zhǎng)和y1>y2時(shí)x的取值范圍.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com