
【題目】如圖,在正方形ABCD中,點E在對角線AC上,點F在邊BC上,連接BE、DF,DF交對角線AC于點G,且DE=DG.
(1)求證:AE=CG;
(2)試判斷BE和DF的位置關系,并說明理由.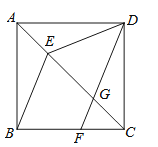
【答案】解:(1)證明:在正方形ABCD中,
∵AD=CD,
∴∠DAE=∠DCG,
∵DE=DG,
∴∠DEG=∠DGE,
∴∠AED=∠CGD.
在△AED和△CGD中,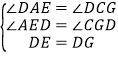
∴△AED≌△CGD(AAS),
∴AE=CG.
(2)解法一:BE∥DF,理由如下:
在正方形ABCD中,AB∥CD,
∴∠BAE=∠DCG.
在△AEB和△CGD中,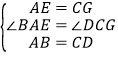
∴△AEB≌△CGD(SAS),
∴∠AEB=∠CGD.
∵∠CGD=∠EGF,
∴∠AEB=∠EGF,
∴BE∥DF.
解法二:BE∥DF,理由如下:
在正方形ABCD中,
∵AD∥FC,
∴![]() =
=![]() .
.
∵CG=AE,
∴AG=CE.
又∵在正方形ABCD中,AD=CB,
∴![]() =
=![]() .
.
又∵∠GCF=∠ECB,
∴△CGF∽△CEB,
∴∠CGF=∠CEB,
∴BE∥DF.
【解析】(1)先證∠AED=∠CGD,再證明△ADE≌△CDG,根據全等三角形的對應邊相等即可得出結論;
(2)先證明△AEB≌△CGD,得出對應角相等∠AEB=∠CGD,得出∠AEB=∠EGF,即可證出平行線.


科目:初中數學 來源: 題型:
【題目】如圖,陽光下,小亮的身高如圖中線段AB所示,他在地面上的影子如圖中線段BC所示,線段DE表示旗桿的高,線段FG表示一堵高墻.
(1)請你在圖中畫出旗桿在同一時刻陽光照射下形成的影子,并用線段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗桿的高DE=15m,旗桿與高墻的距離EG=16m,請求出旗桿的影子落在墻上的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋里裝有分別標有漢字“美”、“麗”、“南”、“山”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先攪拌均勻再摸球.
(1)若從中任取一個球,求摸出球上的漢字剛好是“美”的概率;
(2)甲從中任取一球,不放回,再從中任取一球,請用樹狀圖或列表法,求甲取出的兩個球上的漢字恰能組成“美麗”或“南山”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店因換季將某種服裝打折銷售,如果每件服裝按標價的5折出售將虧20元,而按標價的8折出售將賺40元,設每件服裝的標價是x元,則可列方程為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
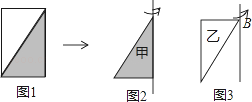
【題目】如圖1,把一張長10厘米、寬6厘米的長方形紙板分成兩個相同的直角三角形.
(1)甲三角形(如圖2)旋轉一周,可以形成一個怎樣的幾何體?它的體積是多少立方米?
(2)乙三角形(如圖3)旋轉一周,可以形成一個怎樣的幾何體?它的體積是多少立方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,各地“廣場舞”噪音干擾的問題備受關注,相關人員對本地區15﹣65歲年齡段的500名市民進行了隨機調查,在調查過程中對“廣場舞”噪音干擾的態度有以下五種:A:沒影響;B:影響不大;C:有影響,建議做無聲運動,D:影響很大,建議取締;E:不關心這個問題,將調查結果繪統計整理并繪制成如下兩幅不完整的統計圖.

請根據以上信息解答下列問題:
(1)填空m=________,態度為C所對應的圓心角的度數為________;
(2)補全條形統計圖;
(3)若全區15﹣65歲年齡段有20萬人,估計該地區對“廣場舞”噪音干擾的態度為B的市民人數;
(4)若在這次調查的市民中,從態度為A的市民中抽取一人的年齡恰好在年齡段15﹣35歲的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com