
如圖,已知點A(−3,5)在拋物線y= x2+c的圖象上,點P從拋物線的頂點Q出發,沿y軸以
x2+c的圖象上,點P從拋物線的頂點Q出發,沿y軸以
每秒1個單位的速度向正方向運動,連結AP并延長,交拋物線于點B,分別過點A、B作x軸的垂線,垂
足為C、D,連結AQ、BQ.
(1)求拋物線的解析式;
(2)當A、Q、B三點構成以AQ為直角邊的直角三角形時,求點P離開點Q多少時間?
(3)試探索當AP、AC、BP、BD與一個平行四邊形的四條邊對應相等(即這四條線段能構成平行四邊形)時,點P離開點Q的時刻.

(1)把A(−3,5)代入得:5= ´9+c,
´9+c,
∴c= .
.
(2)①若AQ⊥BQ,過點Q作MN⊥y軸,

可證△AMQ∽△QNB.
∵AM=AC−MC= ,MQ=3,
,MQ=3,
∴ .
.
設B(3k,2k+ ),
),
代入拋物線解析式得:k= ,即B(
,即B( ,
, ).
).
∴直線AB的解析式為: .
.
∴OP=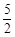 ,∴PQ=2.
,∴PQ=2.
②若AQ⊥AB,

∵AC∥PQ,可證△AMQ∽△QAP,
又由勾股定理得AQ= .
.
∴PQ= .
.
∴對應的時刻t為:2或 .
.
(3)①若AC=BD,AP=BP,
此時點A與點B關于y軸對稱,
∴OP=AC=5,
∴PQ=4 .
.
②若AC=AP,
設P(0,y),則:9+(y−5)2=25,
解之得,y=1,即OP=1.
∴PQ= .
.
此時,直線AP解析式為: .
.
與拋物線的交點B為( ,
, ),
),
∴PB= =BD.
=BD.
∴滿足條件的時刻為: 和4
和4 .
.
【解析】(1)把A點坐標代入就得到拋物線的解析式;
(2)分AQ⊥BQ, AQ⊥AB兩種情況進行討論;
(3)分AC=BD、AC=AP兩種情況進行討論。


科目:初中數學 來源: 題型:
 如圖,已知點A、B、C、D均在已知圓上,AD∥BC,AC平分∠BCD,∠ADC=120°,四邊形ABCD的周長為10cm.圖中陰影部分的面積為( )
如圖,已知點A、B、C、D均在已知圓上,AD∥BC,AC平分∠BCD,∠ADC=120°,四邊形ABCD的周長為10cm.圖中陰影部分的面積為( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知點D為△ABC中AC邊上一點,且AD:DC=3;4,設
如圖,已知點D為△ABC中AC邊上一點,且AD:DC=3;4,設| BA |
| a |
| BC |
| b |
| BD |
| a |
| b |
| a |
| b |
| BD |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com