
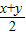 ,G=
,G=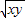 ,
,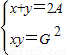 ,
,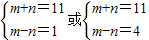 (不合)
(不合)

科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源: 題型:
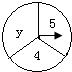
| 指針停靠的扇形內的數字 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出現的次數 | x | 18 | 6 | 5 | 10 | 15 |
查看答案和解析>>
科目:初中數學 來源: 題型:
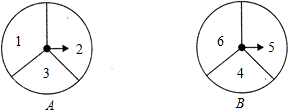
 (2013•武漢模擬)有兩個可以自由轉動的質地均勻轉盤都被分成了3.個全等的扇形,在每一扇形內均標有不同的自然數,如圖所示,轉動轉盤,兩個轉盤停止后觀察并記錄兩個指針所指扇形內的數字(若指針停在扇形的邊線上,當作指向上邊的扇形).
(2013•武漢模擬)有兩個可以自由轉動的質地均勻轉盤都被分成了3.個全等的扇形,在每一扇形內均標有不同的自然數,如圖所示,轉動轉盤,兩個轉盤停止后觀察并記錄兩個指針所指扇形內的數字(若指針停在扇形的邊線上,當作指向上邊的扇形).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com