
【題目】如圖,在矩形ABCD中,已知AB=2 ![]() ,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
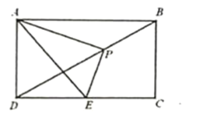
(1)求證:∠PAD=∠PEC;
(2)當點P是BD的中點時,求DE的值;
(3)在點P運動過程中,當DE= ![]() 時,求BP的值.
時,求BP的值.
【答案】(1)見解析;(2)![]() (3)
(3)![]()
【解析】
(1)利用四邊形的內角和和三角形外角的性質得∠DEP+∠DAP=180°,∠DEP+∠PEC=180°,再利用同角的補角相等可得結論;
(2)連接AC,交BD于P.先利用特殊角的三角函數值求出∠ADB=60°,再利用對角線的性質可得PA=PD,故△ADP為等邊三角形,則AP=AD=2;然后易證Rt△ADE≌Rt△APE,可得∠DAE=∠PAE=30°,進而在Rt△ADE中利用tan∠DAE的正切求解即可;
(3)作PG⊥AB于G,GP的延長線交DC于H,得四邊形ADGH是矩形,PG⊥DC,則GH=BC=2;設PG=a,則PH=GH﹣PH=2﹣a,在Rt△BGP中利用tan∠PBG表示出BG和AG;然后易證△AGP∽△PHE,利用相似三角形的對應邊成比例列出關于a比例方程并求解,即可利用BP=2PG=2a計算即可.
解:(1)證明:∵PE⊥AP,
∴∠APE=90°,
∵四邊形ABCD是矩形,
∴∠ADC=90°,
在四邊形ADEP中∠ADE+∠DEP+∠APE+∠DAP=360°,
∴∠DEP+∠DAP=360°-90°-90°=180°,
又∵∠DEP+∠PEC=180°,
∴∠PAD=∠PEC;
(2)解:∵四邊形ABCD是矩形,AB=![]() ,AD=2,
,AD=2,
∴![]() ,
,
∴∠BDA=60°,
連接AC,
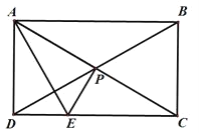
∵點P是BD的中點,
∴點P為AC與BD的交點,
∴△ADP為等邊三角形,
∴AP=AD=2,
在Rt△ADE和Rt△APE中![]() ,
,
∴Rt△ADE≌Rt△APE(HL),
∴∠DAE=∠PAE=30°,
∴![]() ,
,
∴ ![]() ;
;
(3)解:如圖,過點P作PG⊥AB于G,GP的延長線交DC于H,四邊形ABCD是矩形,
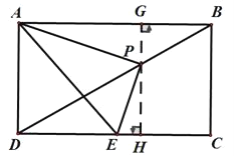
∴PG⊥DC,
∴GH=BC=2,
設PG=a,則PH=GH﹣PH=2﹣a,
在Rt△BGP中,tan∠PBG=![]() ,
,
∴BG=![]() PG=
PG=![]() a,
a,
∴AG=AB-BG=2![]() -
-![]() a=
a=![]() (2-a),
(2-a),
EH=DH-DE=2![]() -
-![]() a-
a-![]() =
=![]() -
-![]() a,
a,
∵PG⊥DC,
∴∠APG+∠EPH=90°,
∵∠APG+∠PAG=90°,
∴∠EPH=∠PAG,
∵∠AGP=∠PHE=90°,
∴△AGP∽△PHE,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴BP=2PG=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在一個可以自由轉動的轉盤中,指針位置固定,三個扇形的面積都相等,且分別標有數字1,2,3.
(1)小明轉動轉盤一次,當轉盤停止轉動時,指針所指扇形中的數字是奇數的概率為 ;
(2)小明先轉動轉盤一次,當轉盤停止轉動時,記錄下指針所指扇形中的數字;接著再轉動轉盤一次,當轉盤停止轉動時,再次記錄下指針所指扇形中的數字,求這兩個數字之和是3的倍數的概率(用畫樹狀圖或列表等方法求解).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】太陽能光伏發電因其清潔、安全、便利、高效等特點,已成為世界各國普遍關注和重點發展的新興產業,如圖是太陽能電池板支撐架的截面圖,其中的粗線表示支撐角鋼,太陽能電池板與支撐角鋼AB的長度相同,均為300cm,AB的傾斜角為![]() ,BE=CA=50cm,支撐角鋼CD,EF與底座地基臺面接觸點分別為D,F,CD垂直于地面,
,BE=CA=50cm,支撐角鋼CD,EF與底座地基臺面接觸點分別為D,F,CD垂直于地面,![]() 于點E.兩個底座地基高度相同(即點D,F到地面的垂直距離相同),均為30cm,點A到地面的垂直距離為50cm,求支撐角鋼CD和EF的長度各是多少cm(結果保留根號)
于點E.兩個底座地基高度相同(即點D,F到地面的垂直距離相同),均為30cm,點A到地面的垂直距離為50cm,求支撐角鋼CD和EF的長度各是多少cm(結果保留根號)


查看答案和解析>>
科目:初中數學 來源: 題型:
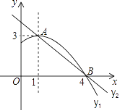
【題目】如圖是拋物線y1=ax2+bx+c(a≠0)圖象的一部分,拋物線的頂點坐標A(1,3),與x軸的一個交點B(4,0),直線y2=mx+n(m≠0)與拋物線交于A,B兩點,下列結論: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有兩個相等的實數根;④拋物線與x軸的另一個交點是(﹣1,0);⑤當1<x<4時,有y2<y1 ,
其中正確的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解朝陽社區![]() 歲居民最喜歡的支付方式,某興趣小組對社區內該年齡段的部分居民展開了隨機問卷調查(每人只能選擇其中一項),并將調查數據整理后繪成如下兩幅不完整的統計圖.請根據圖中信息解答下列問題:
歲居民最喜歡的支付方式,某興趣小組對社區內該年齡段的部分居民展開了隨機問卷調查(每人只能選擇其中一項),并將調查數據整理后繪成如下兩幅不完整的統計圖.請根據圖中信息解答下列問題:
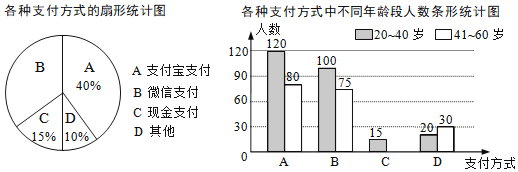
(1)求參與問卷調查的總人數.
(2)補全條形統計圖.
(3)該社區中![]() 歲的居民約8000人,估算這些人中最喜歡微信支付方式的人數.
歲的居民約8000人,估算這些人中最喜歡微信支付方式的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() x2+
x2+![]() x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
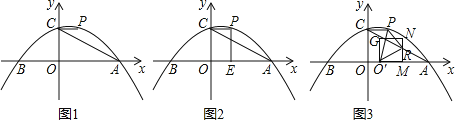
(1)求點P的坐標及直線AC的解析式;
(2)如圖2,過點P作x軸的垂線,垂足為E,將線段OE繞點O逆時針旋轉得到OF,旋轉角為α(0°<α<90°),連接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
(3)如圖3,點M為線段OA上一點,以OM為邊在第一象限內作正方形OMNG,當正方形OMNG的頂點N恰好落在線段AC上時,將正方形OMNG沿x軸向右平移,記平移中的正方形OMNG為正方形O′MNG,當點M與點A重合時停止平移.設平移的距離為t,正方形O′MNG的邊MN與AC交于點R,連接O′P、O′R、PR,是否存在t的值,使△O′PR為直角三角形?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的半圓交AC于點D,交BC于點E,延長AE至點F,使EF=AE,連接FB、FC.
(1)求證:四邊形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圓的面積.
,BE=1,求半圓的面積.
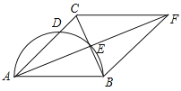
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著社會經濟的發展,汽車逐漸走入平常百姓家.某數學興趣小組隨機抽取了我市某單位部分職工進行調查,對職工購車情況分4類(A:車價40萬元以上;B:車價在20—40萬元;C:車價在20萬元以下;D:暫時未購車)進行了統計,并將統計結果繪制成以下條形統計圖和扇形統計圖.請結合圖中信息解答下列問題:
(1)調查樣本人數為__________,樣本中B類人數百分比是_______,其所在扇形統計圖中的圓心角度數是________;
(2)把條形統計圖補充完整;
(3)該單位甲、乙兩個科室中未購車人數分別為2人和3人,現從中選2人去參觀車展,用列表或畫樹狀圖的方法,求選出的2人來自不同科室的概率.
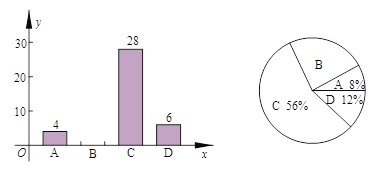
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com