
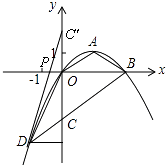
【題目】如圖,頂點為A( ![]() ,1)的拋物線經過坐標原點O,與x軸交于點B.
,1)的拋物線經過坐標原點O,與x軸交于點B.
(1)求拋物線對應的二次函數的表達式;
(2)過B作OA的平行線交y軸于點C,交拋物線于點D,求證:△OCD≌△OAB;
(3)在x軸上找一點P,使得△PCD的周長最小,求出P點的坐標.
【答案】
(1)
解:∵拋物線頂點為A( ![]() ,1),
,1),
設拋物線解析式為y=a(x﹣ ![]() )2+1,
)2+1,
將原點坐標(0,0)在拋物線上,
∴0=a( ![]() )2+1
)2+1
∴a=﹣ ![]() .
.
∴拋物線的表達式為:y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:令y=0,得 0=﹣ ![]() x2+
x2+ ![]() x,
x,
∴x=0(舍),或x=2 ![]()
∴B點坐標為:(2 ![]() ,0),
,0),
設直線OA的表達式為y=kx,
∵A( ![]() ,1)在直線OA上,
,1)在直線OA上,
∴ ![]() k=1,
k=1,
∴k= ![]() ,
,
∴直線OA對應的一次函數的表達式為y= ![]() x.
x.
∵BD∥AO,
設直線BD對應的一次函數的表達式為y= ![]() x+b,
x+b,
∵B(2 ![]() ,0)在直線BD上,
,0)在直線BD上,
∴0= ![]() ×2
×2 ![]() +b,
+b,
∴b=﹣2,
∴直線BD的表達式為y= ![]() x﹣2.
x﹣2.
由 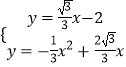
得交點D的坐標為(﹣ ![]() ,﹣3),
,﹣3),
令x=0得,y=﹣2,
∴C點的坐標為(0,﹣2),
由勾股定理,得:OA=2=OC,AB=2=CD,OB=2 ![]() =OD.
=OD.
在△OAB與△OCD中,
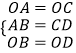 ,
,
∴△OAB≌△OCD.
(3)
解:點C關于x軸的對稱點C'的坐標為(0,2),
∴C'D與x軸的交點即為點P,它使得△PCD的周長最小.
過點D作DQ⊥y,垂足為Q,
∴PO∥DQ.
∴△C'PO∽△C'DQ.
∴ ![]() ,
,
∴ ![]() ,
,
∴PO= ![]() ,
,
∴點P的坐標為(﹣ ![]() ,0)
,0)
【解析】(1)用待定系數法求出拋物線解析式,(2)先求出直線OA對應的一次函數的表達式為y= ![]() x.再求出直線BD的表達式為y=
x.再求出直線BD的表達式為y= ![]() x﹣2.最后求出交點坐標C,D即可;(3)先判斷出C'D與x軸的交點即為點P,它使得△PCD的周長最小.作輔助線判斷出△C'PO∽△C'DQ即可.
x﹣2.最后求出交點坐標C,D即可;(3)先判斷出C'D與x軸的交點即為點P,它使得△PCD的周長最小.作輔助線判斷出△C'PO∽△C'DQ即可.


科目:初中數學 來源: 題型:
【題目】某校要將一塊長為a米,寬為b米的長方形空地設計成花園,現有如下兩種方案供選擇.
方案一:如圖1,在空地上橫、豎各鋪一條寬為4米的石子路,其余空地種植花草.
方案二:如圖2,在長方形空地中留一個四分之一圓和一個半圓區域種植花草,其余空地鋪筑成石子路.
(1) 分別表示這兩種方案中石子路(圖中陰影部分)的面積(若結果中含有π,則保留)
(2) 若a=30,b=20,該校希望多種植物美化校園,請通過計算選擇其中一種方案(π取3.14).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明參加某網店的“翻牌抽獎”活動,如圖,4張牌分別對應價值5,10,15,20(單位:元)的4件獎品. 
(1)如果隨機翻1張牌,那么抽中20元獎品的概率為 .
(2)如果隨機翻2張牌,且第一次翻過的牌不再參加下次翻牌,請用列表或畫樹狀圖的方法求出所獲獎品總值不低于30元的概率為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】雞兔同籠問題是我國古代著名趣題之一,大約在 1500 年前,《孫子算經》中就記載了這個有趣的問題.書中是這樣敘述的:“今有雉兔同籠,上有三十五頭,下有九十四足,問雉兔各幾何?”這四句話的意思是:有若干只雞、兔同在一個籠子里,從上上面數,有 35 個頭;從下面數,有 94 只腳 .求籠中各有幾只雞和兔?經計算可得( )

A. 雞 20 只,兔 15 只 B. 雞 12 只,兔 23 只
C. 雞 15 只,兔 20 只 D. 雞 23 只,兔 12 只
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數 ![]() 的圖象交于A(﹣2,1),B(1,n)兩點.
的圖象交于A(﹣2,1),B(1,n)兩點.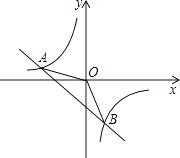
(1)試確定上述反比例函數和一次函數的表達式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七年級⑴班想買一些運動器材供班上同學陽光體育活動使用,班主任安排班長去商店買籃球和排球,下面是班長與售貨員的對話:
班長:阿姨,您好! 售貨員:同學,你好,想買點什么?

⑴根據這段對話,你能算出籃球和排球的單價各是多少嗎?
⑵六一兒童節店里搞活動有兩種套餐,1、套裝打折:五個籃球和五個排球為一套裝,套裝打 八折:2、滿減活動:999 減 100,1999 減 200;兩種活動不重復參與,學校需要 15個籃球,13 個排球作為獎品,請問如何安排購買更劃算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
我們知道:一條線段有兩個端點,線段![]() 和線段
和線段![]() 表示同一條線段. 若在直線
表示同一條線段. 若在直線![]() 上取了三個不同的點,則以它們為端點的線段共有 條;若取了四個不同的點,則共有線段 條;…;依此類推,取了
上取了三個不同的點,則以它們為端點的線段共有 條;若取了四個不同的點,則共有線段 條;…;依此類推,取了![]() 個不同的點,共有線段條.(用含
個不同的點,共有線段條.(用含![]() 的代數式表示)
的代數式表示)
類比探究:
以一個銳角的頂點為端點向這個角的內部引射線.
(1)若引出兩條射線,則所得圖形中共有 個銳角;
(2)若引出![]() 條射線,則所得圖形中共有 個銳角.(用含
條射線,則所得圖形中共有 個銳角.(用含![]() 的代數式表示)
的代數式表示)
拓展應用:
一條鐵路上共有8個火車站,若一列火車往返過程中必須停靠每個車站,則鐵路局需為這條線路準備多少種車票?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC的底邊AB在x軸上,點B與原點O重合,已知點A(﹣2,0),AC= ![]() ,將△ABC沿x軸向右平移,當點C的對應點C1落在直線y=2x﹣4上時,則平移的距離是( )
,將△ABC沿x軸向右平移,當點C的對應點C1落在直線y=2x﹣4上時,則平移的距離是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八(2)班組織了一次經典誦讀比賽,甲、乙兩隊各10人的比賽成績如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲隊成績的中位數是 分,乙隊成績的眾數是 分;
(2)計算乙隊的平均成績和方差;
(3)已知甲隊成績的方差是1.4,則成績較為整齊的是 隊.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com