
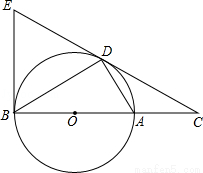
如圖,D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.
(1)求證:CD2=CA•CB;
(2)求證:CD是⊙O的切線;
(3)過點B作⊙O的切線交CD的延長線于點E,若BC=12,tan∠CDA=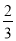 ,求BE的長.
,求BE的長.
(1)證明見解析;(2)證明見解析;(3)5.
【解析】
試題分析:(1)通過相似三角形(△ADC∽△DBC)的對應邊成比例來證得結論;
(2)如圖,連接OD.欲證明CD是⊙O的切線,只需證明OD⊥CD即可;
(3)通過相似三角形△EBC∽△ODC的對應邊成比例列出關于BE的方程,通過解方程來求線段BE的長度即可.
試題解析:(1)證明:∵∠CDA=∠CBD,∠C=∠C,
∴△ADC∽△DBC,
∴ ,即CD2=CA•CB;
,即CD2=CA•CB;
(2)證明:如圖,連接OD.
∵AB是⊙O的直徑,
∴∠ADB=90°,
∴∠1+∠3=90°.
∵OA=OD,
∴∠2=∠3,
∴∠1+∠2=90°.
又∠CDA=∠CBD,即∠4=∠1,
∴∠4+∠2=90°,即∠CDO=90°,
∴OD⊥CD.
又∵OD是⊙O的半徑,
∴CD是⊙O的切線;
(3)【解析】
如圖,連接OE.
∵EB、CD均為⊙O的切線,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA= ,
,
∴tan∠OEB= ,
,
∵∠ODC=∠EBC=90°,∠C=∠C,
∴Rt△CDO∽Rt△CBE,
∴ ,
,
∴CD=8,
在Rt△CBE中,設BE=x,
∴(x+8)2=x2+122,
解得x=5.
即BE的長為5.
考點:1.切線的判定;2.相似三角形的判定與性質.


科目:初中數學 來源:2013-2014學年北京市大興區中考一模數學試卷(解析版) 題型:解答題
如果三角形有一邊上的中線恰好等于這邊的長,那么稱這個三角形為“勻稱三角形”.
(1)已知:如圖1,在△ABC中,∠C=90°,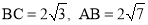 .
.
求證:△ABC是“勻稱三角形”;
(2)在平面直角坐標系xoy中,如果三角形的一邊在x軸上,且這邊的中線恰好等于這邊的長,我們又稱這個三角形為“水平勻稱三角形”.如圖2,現有10個邊長是1的小正方形組成的長方形區域記為G, 每個小正方形的頂點稱為格點,A(3,0),B(4,0),若C、D(C、D兩點與O不重合)是x軸上的格點,且點C在點A的左側.在G內使△PAC與△PBD都是“水平勻稱三角形”的點P共有幾個?其中是否存在橫坐標為整數的點P,如果存在請求出這個點P的坐標,如果不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年北京市大興區中考一模數學試卷(解析版) 題型:選擇題
若一列不全為零的數除了第一個數和最后一個數外,每個數都等于前后與它相鄰的兩數之和,則稱這列數具有“波動性質”.已知一列數共有18個,且具有“波動性質”,則這18個數的和為( )
A.-64 B.0 C.18 D.64
查看答案和解析>>
科目:初中數學 來源:2013-2014學年內蒙古滿洲里市九年級三月月考數學試卷(解析版) 題型:填空題
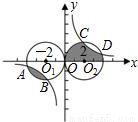
如圖,半徑為2的兩圓⊙O1和⊙O2均與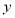 軸相切于點
軸相切于點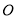 ,反比例函數
,反比例函數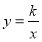 (
(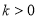 )的圖像與兩圓分別交于點A、B、C、D,則圖中陰影部分的面積是 .
)的圖像與兩圓分別交于點A、B、C、D,則圖中陰影部分的面積是 .
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.P點在△ABC內 |
| B.P點在BC邊上 |
| C.P點在△ABC外 |
| D.P點位置與BC邊的長度有關 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com