
【題目】如圖1,直線AB∥CD,直線EF交AB于點(diǎn)E,交CD于點(diǎn)F,點(diǎn)G和點(diǎn)H分別是直線AB和CD上的動點(diǎn),作直線GH,EI平分∠AEF,HI平分∠CHG,EI與HI交于點(diǎn)I.
(1)如圖,點(diǎn)G在點(diǎn)E的左側(cè),點(diǎn)H在點(diǎn)F的右側(cè),若∠AEF=70°,∠CHG=60°,求∠ETH的度數(shù).
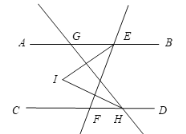
(2)如圖,點(diǎn)G在點(diǎn)E的右側(cè),點(diǎn)H也在點(diǎn)F的右側(cè),若∠AEF=![]() ,∠CHG=β,其他條件不變,求∠ETH的度數(shù).
,∠CHG=β,其他條件不變,求∠ETH的度數(shù).
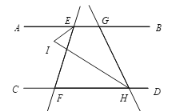
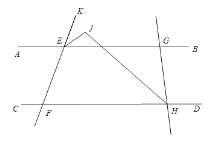
(3)如圖,點(diǎn)G在點(diǎn)E的右側(cè),點(diǎn)H也在點(diǎn)F的右側(cè),∠GHC的平分線HJ交∠KEG的平分線EJ于點(diǎn)J.其他條件不變,若∠AEF=![]() ,∠CHG=β,求∠EJH的度數(shù).
,∠CHG=β,求∠EJH的度數(shù).
【答案】(1)65°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)過點(diǎn)I作IM∥AB ,由角平分線的性質(zhì)得到∠AEI=35°,∠CHI=30°,
根據(jù)平行線的性質(zhì),由IM∥AB得到∠MIE=∠AEI=35°,由AB∥CD,IM∥AB
可得∠MIH=∠CHI=30°,再由∠EIH=∠MIE+∠MIH計算即可得到答案;
(2)過點(diǎn)I作IM∥AB,由角平分線的性質(zhì)得到∠AEI=![]() ,∠CHI=
,∠CHI=![]() ,根據(jù)平行線的性質(zhì)由IM∥AB可得∠MIE=∠AEI=
,根據(jù)平行線的性質(zhì)由IM∥AB可得∠MIE=∠AEI=![]() ,由AB∥CD,IM∥AB得到IM∥CD,結(jié)合題意得到∠EIH=∠MIE+∠MIH計算即可得到答案;
,由AB∥CD,IM∥AB得到IM∥CD,結(jié)合題意得到∠EIH=∠MIE+∠MIH計算即可得到答案;
(3)過點(diǎn)J作MN∥AB ,由角平分線的性質(zhì)得到∠JEG=![]() ,∠JHF=
,∠JHF=![]() ,根據(jù)平行線的性質(zhì)由MN∥AB得到∠MJE=∠JEG =
,根據(jù)平行線的性質(zhì)由MN∥AB得到∠MJE=∠JEG =![]() ,由AB∥CD,MN∥AB得到MN∥CD,結(jié)合題意得到∠EJH=180°-∠MJE-∠NJH,計算即可得到答案.
,由AB∥CD,MN∥AB得到MN∥CD,結(jié)合題意得到∠EJH=180°-∠MJE-∠NJH,計算即可得到答案.
(1)解:過點(diǎn)I作IM∥AB

∵EI平分∠AEF,HI平分∠CHG,∠AEF=70°,∠CHG=60°,
∴∠AEI=35°,∠CHI=30°
∵IM∥AB
∴∠MIE=∠AEI=35°
∵AB∥CD,IM∥AB
∴IM∥CD
∴∠MIH=∠CHI=30°
∴∠EIH=∠MIE+∠MIH=35°+30°=65°
(2)解:過點(diǎn)I作IM∥AB

∵EI平分∠AEF,HI平分∠CHG,∠AEF=![]() ,∠CHG=β,
,∠CHG=β,
∴∠AEI=![]() ,∠CHI=
,∠CHI=![]()
∵IM∥AB
∴∠MIE=∠AEI=![]()
∵AB∥CD,IM∥AB
∴IM∥CD
∴∠MIH=∠CHI=![]()
∴∠EIH=∠MIE+∠MIH=![]() +
+![]()
(3)解:過點(diǎn)J作MN∥AB
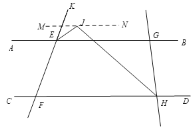
∵∠AEF=![]()
∴∠KEB=![]()
∵EJ平分∠KEB,HJ平分∠CHG,∠KEB =![]() ,∠CHG=β,
,∠CHG=β,
∴∠JEG=![]() ,∠JHF=
,∠JHF=![]()
∵MN∥AB
∴∠MJE=∠JEG =![]()
∵AB∥CD,MN∥AB
∴MN∥CD
∴∠NJH=∠CHJ=![]()
∴∠EJH=180°-∠MJE-∠NJH=180°-![]() -
-![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小華將一條直角邊長為1的一個等腰直角三角形紙片(如圖1),沿它的對稱軸折疊1次后得到一個等腰直角三角形(如圖2),再將圖2的等腰直角三角形沿它的對稱軸折疊后得到一個等腰直角三角形(如圖3),則圖3中的等腰直角三角形的一條腰長為_________;同上操作,若小華連續(xù)將圖1的等腰直角三角形折疊n次后所得到的等腰直角三角形(如圖n+1)的一腰長為_________.
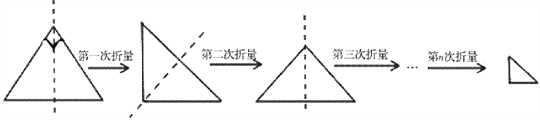
圖1 圖2 圖3 圖n+1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在括號內(nèi)注明說理依據(jù).如圖已知∠B=∠D,∠1=∠2,試猜想∠A與∠C的大小關(guān)系,并說明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代換)
∴AB∥CD
∴∠A=∠C .
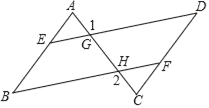
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,點(diǎn)![]() 、
、![]() 、
、![]() 在同一直線上,
在同一直線上,![]() 是
是![]() 的平分線,
的平分線,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度數(shù)(請寫出解題過程).
的度數(shù)(請寫出解題過程).
(2)如以![]() 為一邊,在
為一邊,在![]() 的外部畫
的外部畫![]() ,問邊
,問邊![]() 與邊
與邊![]() 成一直線嗎?請說明理由.
成一直線嗎?請說明理由.
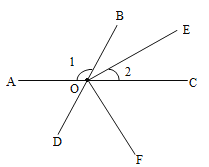
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2019年7月7日,國務(wù)院辦公廳發(fā)布《國務(wù)院辦公廳關(guān)于同意山西省承辦2019年第二屆全國青年運(yùn)動會的函》,本屆運(yùn)動會初步確定在2019年8月至9月份舉辦,歷時8至10天,預(yù)計約有55個代表團(tuán)參賽,為了讓每位運(yùn)動員在比賽之余能有一個較好的療養(yǎng)鍛煉的環(huán)境,二青會籌備委員會,決定從某公司采購甲、乙兩種健身器材共800件,已知購買2件甲器材與3件乙器材的價格相同,購買3件甲器材比2件乙器材的價格多1500元.
(1) 每件甲乙兩種器材各多少元?
(2) 若購買甲、乙兩種器材的價格不超過54萬元,則最多可購買甲種器材多少件?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】同學(xué)們都知道,![]() 表示5與 -2之差的絕對值,實際上也可以理解為 5 與 -2兩數(shù)在數(shù)軸上所對的兩點(diǎn)之間的距離,則使得
表示5與 -2之差的絕對值,實際上也可以理解為 5 與 -2兩數(shù)在數(shù)軸上所對的兩點(diǎn)之間的距離,則使得![]() 這樣的整數(shù)
這樣的整數(shù)![]() 有____個.
有____個.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 、
、![]() 是弧
是弧![]() (異于
(異于![]() 、
、![]() )上兩點(diǎn),
)上兩點(diǎn),![]() 是弧
是弧![]() 上一動點(diǎn),
上一動點(diǎn),![]() 的角平分線交
的角平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 的平分線交
的平分線交![]() 于點(diǎn)
于點(diǎn)![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 運(yùn)動到點(diǎn)
運(yùn)動到點(diǎn)![]() 時,則
時,則![]() 、
、![]() 兩點(diǎn)的運(yùn)動路徑長的比是( )
兩點(diǎn)的運(yùn)動路徑長的比是( )
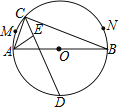
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
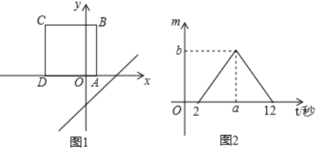
【題目】如圖1,將正方形ABCD置于平面直角坐標(biāo)系中,其中AD邊在x軸上,其余各邊均與坐標(biāo)軸平行,直線l:y=x﹣3沿x軸的負(fù)方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形ABCD的邊所截得的線段長為m,平移的時間為t(秒),m與t的函數(shù)圖象如圖2所示,則圖2中b的值為( )
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com