
���}Ŀ����(du��)���Ă�(g��)��(sh��)��![]() ��
��![]() ��
��![]() ��
��![]() �����ķN�\(y��n)����
�����ķN�\(y��n)����![]() ��
��![]() ��
��![]() ��
��![]() ��������ʽ���
��������ʽ���
��1�����@�Ă�(g��)��(sh��)�ĺͣ�
��2�����@�Ă�(g��)��(sh��)���x���ɂ�(g��)��(sh��)����Ҫ���M(j��n)������Ӌ(j��)�㣬ʹ�ã�
�كɔ�(sh��)��ĽY(ji��)����С��
�ڃɔ�(sh��)�e�ĽY(ji��)�����
��3�����@�Ă�(g��)��(sh��)���x������(g��)��(sh��)�����ķN�\(y��n)�����x���ɷN���M��һ��(g��)��ʽ��ʹ�\(y��n)��Y(ji��)�����ڛ](m��i)�x���ǂ�(g��)��(sh��)��
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ����3��
����3��![]() ���𰸲�Ψһ����
���𰸲�Ψһ����
��������
��1�����}Ŀ�еĔ�(sh��)��(j��)��Ӽ��ɽ���}��
��2���ٸ���(j��)�}Ŀ�еĔ�(sh��)�֣����Ԍ�(xi��)���Y(ji��)����С����ʽ��
�ڸ���(j��)�}Ŀ�еĔ�(sh��)�֣����Ԍ�(xi��)���Y(ji��)��������ʽ��
��3�����}�𰸲�Ψһ����Ҫ�����}�⼴�ɣ�
�⣺��1����-8��+��-2��+1+3=-6��
��2�����}Ŀ�еĔ�(sh��)�ֿɵã�
��![]() ���Y(ji��)������
���Y(ji��)������
��![]() ���Y(ji��)�����
���Y(ji��)�����
��3�����}Ŀ�еĔ�(sh��)�ֿɵã�
![]() ���𰸲�Ψһ����
���𰸲�Ψһ����


 ��x��܇(ch��)ϵ�д�
��x��܇(ch��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��һ�κ���(sh��)![]() �ĈD���c����������(sh��)
�ĈD���c����������(sh��)![]() �ڵ�һ���ĈD����
�ڵ�һ���ĈD����![]() ��
��![]() ���c(di��n)���c
���c(di��n)���c![]() �S�����c(di��n)
�S�����c(di��n)![]() �B��
�B��![]()
��1����������(sh��)�Ľ���ʽ��
��2�����c(di��n)![]() ��
��![]() �S�ϣ���
�S�ϣ���![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
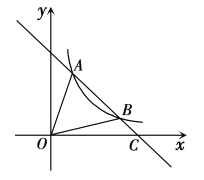
���}Ŀ����D���c(di��n)A���p����(xi��n)y��![]() �ϵĄ�(d��ng)�c(di��n)���B�Y(ji��)AO�����L(zh��ng)���p����(xi��n)���c(di��n)B������(xi��n)��AB�@B형r(sh��)����D(zhu��n)60��õ���(xi��n)��BC���c(di��n)C���p����(xi��n)y��
�ϵĄ�(d��ng)�c(di��n)���B�Y(ji��)AO�����L(zh��ng)���p����(xi��n)���c(di��n)B������(xi��n)��AB�@B형r(sh��)����D(zhu��n)60��õ���(xi��n)��BC���c(di��n)C���p����(xi��n)y��![]() �ϵ��\(y��n)��(d��ng)���tk��____��
�ϵ��\(y��n)��(d��ng)���tk��____��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ֱ��(xi��n)![]() �c
�c![]() �S�����c(di��n)
�S�����c(di��n)![]() ���c
���c![]() �S�����c(di��n)
�S�����c(di��n)![]() ����(j��ng)�^(gu��)
����(j��ng)�^(gu��)![]() ��
��![]() ���c(di��n)�Ē��タ(xi��n)
���c(di��n)�Ē��タ(xi��n)![]() �c
�c![]() �S����һ���c(di��n)
�S����һ���c(di��n)![]() ��
��
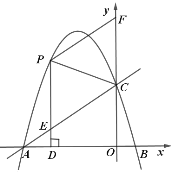
��1����ԓ���タ(xi��n)�ĺ���(sh��)���_(d��)ʽ��
��2��![]() ��ԓ���タ(xi��n)�ϵĄ�(d��ng)�c(di��n)���^(gu��)�c(di��n)
��ԓ���タ(xi��n)�ϵĄ�(d��ng)�c(di��n)���^(gu��)�c(di��n)![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ��
��
�������߅��![]() �����L(zh��ng)
�����L(zh��ng)![]() �c
�c![]() �ĺ���(sh��)���_(d��)ʽ������
�ĺ���(sh��)���_(d��)ʽ������![]() �����ֵ��
�����ֵ��
�ڮ�(d��ng)![]() ���ֵ�r(sh��)����߅��
���ֵ�r(sh��)����߅��![]() �����Σ�
������
���Ƿ�����c(di��n)![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() ����c(di��n)���������c
����c(di��n)���������c![]() ���ƣ������ڣ�Ո(q��ng)����M(m��n)��l�����c(di��n)
���ƣ������ڣ�Ո(q��ng)����M(m��n)��l�����c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����Ъ�(d��)�صĚ���YԴ����Ȼ���ֵă�(y��u)�|(zh��)�������VԪ�д����ƏV�߲˷Nֲ������������g��ij�߲˷Nֲ����ͨ�^(gu��)���ƽ�_(t��i)���߲��N(xi��o)��ȫ��(gu��)���أ��N(xi��o)�������������ԓ���؞�����߲ˮa(ch��n)����Ӌ(j��)����(du��)�ס��҃ɷN��̖(h��o)�߲˴����M(j��n)�и��죬����(j��)�A(y��)�㣬����2��(g��)�N��̖(h��o)�����1��(g��)�ҷN��̖(h��o)��������Y��6�f(w��n)Ԫ������1��(g��)�N��̖(h��o)�����2��(g��)�ҷN��̖(h��o)���ﹲ���Y��48�f(w��n)Ԫ��
��1�������1��(g��)�N��̖(h��o)��1��(g��)�ҷN��̖(h��o)���������Y��քe�Ƕ����f(w��n)Ԫ��
��2����֪����1��(g��)�N��̖(h��o)������Ҫ5�죬����1��(g��)�ҷN��̖(h��o)������Ҫ3�죬ԓ����Ӌ(j��)����126�f(w��n)Ԫ�Y�����һ����(sh��)���ăɷN��̖(h��o)�߲˴����Ҫ�����r(sh��)�g���������^(gu��)50�죬Ո(q��ng)��(w��n)���ЎN���췽�����ķN��������r(sh��)�g��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�Θ�(l��)�@��һ��(g��)ֱ����16�ĈA�·�ˮ�أ���ˮ�ص���߅��һȦ��ˮ�^��������ˮ���钁�タ(xi��n)���ھ�ˮ������3��̎�_(d��)����ߣ��߶Ȟ�5�ף��Ҹ�������ˮ��ǡ���ڇ�ˮ�����ĵ��b���̎�R�ϣ���D��ʾ����ˮƽ����?y��n)?/span>x�S����ˮ�����Ğ�ԭ�c(di��n)����ֱ������(bi��o)ϵ��
��1����ˮ�����ڒ��タ(xi��n)����һ�����֣��ĺ���(sh��)���_(d��)ʽ��
��2���������ڇ�ˮ��(n��i)�S���O(sh��)�����g����ˮ�����⇊ˮ�����˲����ܝ�����1.8��������վ���r(sh��)������xˮ�����Ķ�������?x��n)?n��i)��
��3����(j��ng)�z���u(p��ng)�����Θ�(l��)�@�Q����(du��)��ˮ�O(sh��)ʩ�������O(sh��)Ӌ(j��)���M(j��n)���ڇ���ˮ�����Π׃��ǰ���£���ˮ�ص�ֱ���U(ku��)��32�ף���������ˮ�����ڇ�ˮ�����ı�����ԭ�b���߶Ȳ�׃��̎�R�ϣ�Ո(q��ng)?zh��)����U(ku��)�������ˮ��ˮ�������߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ����ƽ��ֱ������(bi��o)ϵ�У����タ(xi��n)y=ax2+bx+3��(j��ng)�^(gu��)A����3��0����B��1��0�����c(di��n)���cy�S�����c(di��n)C������c(di��n)��D���B��AD���c(di��n)P�Ǿ�(xi��n)��AD��һ��(g��)��(d��ng)�c(di��n)�����cA��D�غϣ����^(gu��)�c(di��n)P��y�S�Ĵ���(xi��n)�������c(di��n)��E���B��AE��
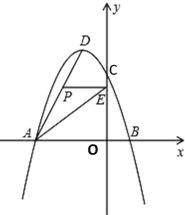
��1�����タ(xi��n)�ĺ���(sh��)����ʽ������(xi��)����c(di��n)D������(bi��o)��
��2�����P�c(di��n)������(bi��o)�飨x��y������PAE����e��S����S�cx֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��ֱ�ӌ�(xi��)����׃��x��ȡֵ�����������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
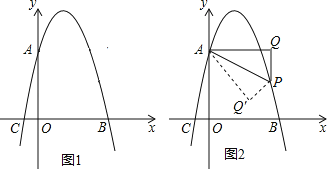
���}Ŀ����D1����֪���タ(xi��n)y����x2+bx+c��y�S���c(di��n)A(0��4)����x�S���c(di��n)B(4��0)���c(di��n)P�ǒ��タ(xi��n)��һ��(d��ng)�c(di��n)��ԇ�^(gu��)�c(di��n)P��x�S�Ĵ���(xi��n)1�����^(gu��)�c(di��n)A��1�Ĵ���(xi��n)�������Q���B��AP��
(1)���タ(xi��n)�ĺ���(sh��)���_(d��)ʽ���c(di��n)C������(bi��o)��
(2)����AQP�ס�AOC�����c(di��n)P�ęM����(bi��o)��
(3)��D2����(d��ng)�c(di��n)Pλ�ڒ��タ(xi��n)�Č�(du��)�Q(ch��ng)�S���҂�(c��)�r(sh��)����APQ��AP��(du��)�ۣ��c(di��n)Q�Č�(du��)��(y��ng)�c(di��n)���c(di��n)Q�䣬Ո(q��ng)ֱ�ӌ�(xi��)����(d��ng)�c(di��n)Q����������(bi��o)�S�ϕr(sh��)�c(di��n)P������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(w��n)�}���������ͬ�Ӵ�С������256��(g��)��ƴ����D1��ʾ��![]() ��һ��(g��)��������Σ�Ո(q��ng)��(w��n)�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)���ق�(g��)С�����Σ�
��һ��(g��)��������Σ�Ո(q��ng)��(w��n)�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)���ق�(g��)С�����Σ�

����(w��n)�}̽�������҂��ȿ��]���º�(ji��n)�ε���r��һ�lֱ��(xi��n)��Խһ��(g��)�����ε���r������D2��
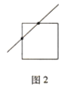
�ĈD���҂����Կ�������(d��ng)һ�lֱ��(xi��n)���^(gu��)һ��(g��)С�����Εr(sh��)���@�lֱ��(xi��n)����c�������ϡ��¡������ėl߅�еăɂ�(g��)߅�ཻ�����Ԯ�(d��ng)һ�lֱ��(xi��n)���^(gu��)һ��(g��)С�����Εr(sh��)���@�lֱ��(xi��n)��(hu��)�c����ij�ɗl߅�a(ch��n)���ɂ�(g��)���c(di��n)��������?x��n)ɂ�(g��)���c(di��n)����c(di��n)�ľ�(xi��n)�Ε�(hu��)ȫ������С������(n��i)��
�@�͆��l(f��)�҂����������ֱ��(xi��n)![]() ��ഩ�^(gu��)���ق�(g��)С�����Σ��҂������D(zhu��n)��ȥ���]��(d��ng)ֱ��(xi��n)
��ഩ�^(gu��)���ق�(g��)С�����Σ��҂������D(zhu��n)��ȥ���]��(d��ng)ֱ��(xi��n)![]() ��Խ��С������ƴ�ɵĴ������Εr(sh��)�����(hu��)�a(ch��n)�����ق�(g��)���c(di��n).Ȼ���ɽ��c(di��n)��(sh��)ȥ�_���ж��ٸ�С��(xi��n)�Σ��M(j��n)��ͨ�^(gu��)��(xi��n)�εĸ���(sh��)�_���������εĂ�(g��)��(sh��)��
��Խ��С������ƴ�ɵĴ������Εr(sh��)�����(hu��)�a(ch��n)�����ق�(g��)���c(di��n).Ȼ���ɽ��c(di��n)��(sh��)ȥ�_���ж��ٸ�С��(xi��n)�Σ��M(j��n)��ͨ�^(gu��)��(xi��n)�εĸ���(sh��)�_���������εĂ�(g��)��(sh��)��
���҂���(l��i)���]![]() �����ε���r����D3����
�������r����D3����
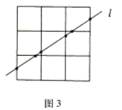
����ֱ��(xi��n)��Խ�����С�����Σ��҂��������O(sh��)ֱ��(xi��n)![]() ���Ϸ������·����^(gu��)һ��(g��)
���Ϸ������·����^(gu��)һ��(g��)![]() �������Σ��҂��ăɂ�(g��)�����(l��i)����ֱ��(xi��n)
�������Σ��҂��ăɂ�(g��)�����(l��i)����ֱ��(xi��n)![]() ���^(gu��)
���^(gu��)![]() �����ε���r��������(l��i)�����@�lֱ��(xi��n)�����������ɴ��^(gu��)����ƽ�еăɗl��(xi��n)�Σ������ҁ�(l��i)�����@�lֱ��(xi��n)���ɴ��^(gu��)����ƽ�е��ėl��(xi��n)�Σ��@��ֱ��(xi��n)
�����ε���r��������(l��i)�����@�lֱ��(xi��n)�����������ɴ��^(gu��)����ƽ�еăɗl��(xi��n)�Σ������ҁ�(l��i)�����@�lֱ��(xi��n)���ɴ��^(gu��)����ƽ�е��ėl��(xi��n)�Σ��@��ֱ��(xi��n)![]() ���ɴ��^(gu��)
���ɴ��^(gu��)![]() �Ĵ��������е����l��(xi��n)�Σ��Ķ�ֱ��(xi��n)
�Ĵ��������е����l��(xi��n)�Σ��Ķ�ֱ��(xi��n)![]() �ϕ�(hu��)�a(ch��n)��6��(g��)���c(di��n)���@6��(g��)���c(di��n)֮�g��5�l��(xi��n)�Σ�ÿ�l��(hu��)����һ��(g��)��ͬ��������(n��i)�����ֱ��(xi��n)
�ϕ�(hu��)�a(ch��n)��6��(g��)���c(di��n)���@6��(g��)���c(di��n)֮�g��5�l��(xi��n)�Σ�ÿ�l��(hu��)����һ��(g��)��ͬ��������(n��i)�����ֱ��(xi��n)![]() ����ܽ�(j��ng)�^(gu��)5��(g��)С�����Σ�
����ܽ�(j��ng)�^(gu��)5��(g��)С�����Σ�
����(w��n)�}��Q����
��1����ͬ�Ӵ�С��С������16��(g��)��ƴ����D4��ʾ��![]() ��һ��(g��)��������Σ������һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)_________��(g��)С�����Σ�
��һ��(g��)��������Σ������һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)_________��(g��)С�����Σ�

��2����ͬ�Ӵ�С��С������256��(g��)��ƴ��![]() ��һ��(g��)���������.�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����Σ�
��һ��(g��)���������.�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������ε�Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����Σ�
��3�������һ�lֱ��(xi��n)���^(gu��)![]() �Ĵ������ε�Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����Σ�
�Ĵ������ε�Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����Σ�
����(w��n)�}��չ����
��4�������һ�lֱ��(xi��n)���^(gu��)![]() �Ĵ��L(zh��ng)���ε�Ԓ(hu��)����D5���������Դ��^(gu��)��(g��)___________С�����Σ�
�Ĵ��L(zh��ng)���ε�Ԓ(hu��)����D5���������Դ��^(gu��)��(g��)___________С�����Σ�

��5�������һ�lֱ��(xi��n)���^(gu��)![]() �Ĵ��L(zh��ng)���ε�Ԓ(hu��)����D6���������Դ��^(gu��)___________��(g��)С�����Σ�
�Ĵ��L(zh��ng)���ε�Ԓ(hu��)����D6���������Դ��^(gu��)___________��(g��)С�����Σ�
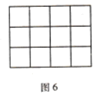
��6�������һ�lֱ��(xi��n)���^(gu��)![]() �Ĵ��L(zh��ng)���ε�Ԓ(hu��)�������Դ��^(gu��)________��(g��)С�����Σ�
�Ĵ��L(zh��ng)���ε�Ԓ(hu��)�������Դ��^(gu��)________��(g��)С�����Σ�
���(l��i)��̽������
�ɶ��S��ƽ���҂�����(li��n)�뵽���S�����w���g��ƽ���е����������ėl߅��(li��n)�뵽�����w�е������ε�����(g��)�棬�(l��i)�����憖(w��n)�}��Q�ķ�����Q����(w��n)�}��
��7����D7��ͬ�Ӵ�С��С�����w8��(g��)��ƴ����D��ʾ��![]() ��һ��(g��)��������w.�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������w��Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����w��
��һ��(g��)��������w.�����һ�lֱ��(xi��n)���^(gu��)�@��(g��)�������w��Ԓ(hu��)�������Դ��^(gu��)___________��(g��)С�����w��
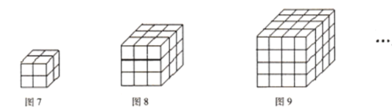
��8�������һ�lֱ��(xi��n)���^(gu��)![]() �Ĵ������w��Ԓ(hu��)�������Դ��^(gu��)_________��(g��)С�����w��
�Ĵ������w��Ԓ(hu��)�������Դ��^(gu��)_________��(g��)С�����w��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com