
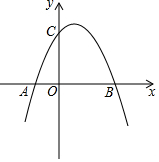 如圖,已知拋物線y=-x2+4x+5與x軸的兩個交點為A、B,與y軸交于點C.
如圖,已知拋物線y=-x2+4x+5與x軸的兩個交點為A、B,與y軸交于點C.分析 (1)對應(yīng)拋物線分別令y=0,x=0解方程即可.
(2)利用配方法即可解決問題.
(3)滿足條件的點有三個,設(shè)M1(m,n).由四邊形ABM1C是平行四邊形,推出BC與AM1互相平分,可得$\frac{-1+m}{2}$=$\frac{0+5}{2}$,$\frac{0+n}{2}$=$\frac{5+0}{2}$,解方程即可解決問題.
解答 解:(1)對應(yīng)拋物線y=-x2+4x+5,令y=0,得-x2+4x+5=0,解得x=-1或5,
∴A(-1,0),B(5,0),
令x=0得y=5,
∴點C坐標(0,5),
∴A(-1,0),B(5,0),C(0,5).
(2)∵y=-x2+4x+5=-(x2-4x)+5=-(x-2)2+9,
∴對稱軸x=2,頂點坐標為(2,9).
(3)如圖,滿足條件的點有三個,設(shè)M1(m,n).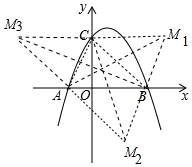
∵四邊形ABM1C是平行四邊形,
∴BC與AM1互相平分,
∴$\frac{-1+m}{2}$=$\frac{0+5}{2}$,$\frac{0+n}{2}$=$\frac{5+0}{2}$,
∴m=6,n=5,
∴M1(6,5),同理可得M2(4,-5),M3(-5,5).
∴滿足條件的點M坐標為(6,5)或(4,-5)或(-5,5).
點評 本題考查二次函數(shù)的綜合題、平行四邊形的性質(zhì)等知識,解題的關(guān)鍵是靈活運用所學(xué)知識解決問題,學(xué)會利用中點坐標公式求點坐標,屬于中考常考題型.


 名牌學(xué)校分層周周測系列答案
名牌學(xué)校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,甲、乙兩人分別從A(1,$\sqrt{3}$),B(6,0)兩點同時出發(fā),點O為坐標原點,甲沿AO方向,乙沿BO方向均以4km/h的速度行駛,th后,甲到達M點,乙到達N點.
如圖,甲、乙兩人分別從A(1,$\sqrt{3}$),B(6,0)兩點同時出發(fā),點O為坐標原點,甲沿AO方向,乙沿BO方向均以4km/h的速度行駛,th后,甲到達M點,乙到達N點.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題

| A. | 68 | B. | 75 | C. | 78 | D. | 88 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在△ABC中,AB=AC=10,點D是BC邊上的一動點(不與B、C重合),∠ADE=∠B=∠α,DE交AB于點E,且tan∠α=$\frac{3}{4}$,有以下的結(jié)論:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE為直角三角形時,BD為8或$\frac{7}{2}$;④0<BE≤5,其中正確的結(jié)論是①③(填入正確結(jié)論的序號)
如圖,在△ABC中,AB=AC=10,點D是BC邊上的一動點(不與B、C重合),∠ADE=∠B=∠α,DE交AB于點E,且tan∠α=$\frac{3}{4}$,有以下的結(jié)論:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE為直角三角形時,BD為8或$\frac{7}{2}$;④0<BE≤5,其中正確的結(jié)論是①③(填入正確結(jié)論的序號)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com