
【題目】實踐探究,解決問題
如圖1,△ABC中,AD為BC邊上的中線,則S△ABD=S△ACD . 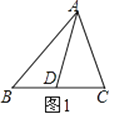
(1)在圖2中,E、F分別為矩形ABCD的邊AD、BC的中點,且AB=4,AD=8,則S陰影=;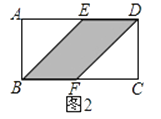
(2)在圖3中,E、F分別為平行四邊形ABCD的邊AD、BC的中點,則S陰影和S平行四邊形ABCD之間滿足的關系式為;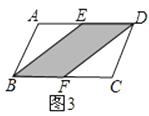
(3)在圖4中,E、F分別為任意四邊形ABCD的邊AD、BC的中點,則S陰影和S四邊形ABCD之間還滿足(2)中的關系式嗎?若滿足,請予以證明,若不滿足,說明理由.
解決問題: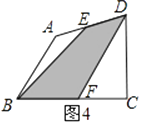
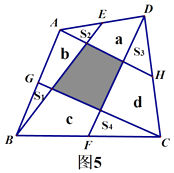
(4)在圖5中,E、G、F、H分別為任意四邊形ABCD的邊AD、AB、BC、CD的中點,并且圖中陰影部分的面積為20平方米,求圖中四個小三角形的面積和(即S1+S2+S3+S4的值).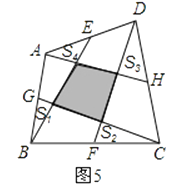
【答案】
(1)16
(2)S陰影= ![]() S平行四邊形ABCD
S平行四邊形ABCD
(3)
解:滿足(2)中的關系式,理由如下:
連接BD,由圖1得S△EBD= ![]() S△ABD 同理S△BDF=
S△ABD 同理S△BDF= ![]() S△BDC
S△BDC
∴S四邊形EBFD=S△EBD+S△BDF= ![]() S四邊形ABCD
S四邊形ABCD
(4)
解:設四邊形的空白區域分別為a,b,c,d
由上述性質可以得出:
a+S2+S3= ![]() S△ACD①,c+S1+S4=
S△ACD①,c+S1+S4= ![]() S△ACB②,b+S2+S1=
S△ACB②,b+S2+S1= ![]() S△ABD③,d+S4+S3=
S△ABD③,d+S4+S3= ![]() S△ACD④,
S△ACD④,
①+②+③+④得,a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四邊形ABCD⑤
而S四邊形ABCD=a+b+c+d+S1+S2+S3+S4+S陰影⑥
所以聯立⑤⑥得S1+S2+S3+S4=S陰影=20平方米.
【解析】解:(1)∵E、F分別為矩形ABCD的邊AD、BC的中點,且AB=4,AD=8,
∴S陰影= ![]() ×8×4=16,
×8×4=16,
所以答案是:16;(2)∵E、F分別為平行四邊形ABCD的邊AD、BC的中點,
∴S陰影= ![]() S平行四邊形ABCD;
S平行四邊形ABCD;
所以答案是:S陰影= ![]() S平行四邊形ABCD;
S平行四邊形ABCD;
【考點精析】本題主要考查了矩形的性質的相關知識點,需要掌握矩形的四個角都是直角,矩形的對角線相等才能正確解答此題.


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點O在對角線AC上,以OA的長為半徑的圓O與AD、AC分別交于點E、F,且∠ACB=∠DCE.
(1)判斷直線CE與⊙O的位置關系,并證明你的結論;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半徑.
,BC=2,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,△ABC的三個頂點坐標分別為A(0,4),B(2,4),C(3,﹣1).
(1)試在平面直角坐標系中,標出A、B、C三點;
(2)求△ABC的面積.
(3)若△A1B1C1與△ABC關于x軸對稱,寫出A1、B1、C1的坐標,并畫出△A1B1C1 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在菱形ABCD中,AC=2,BD=2![]() ,AC,BD相交于點O.
,AC,BD相交于點O.
(1)求邊AB的長;
(2)如圖2,將一個足夠大的直角三角板60°角的頂點放在菱形ABCD的頂點A處,繞點A左右旋轉,其中三角板60°角的兩邊分別與邊BC,CD相交于點E,F,連接EF與AC相交于點G.
①判斷△AEF是哪一種特殊三角形,并說明理由;
②旋轉過程中,當點E為邊BC的四等分點時(BE>CE),求CG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是按規律擺放在墻角的一些小正方體,從上往下分別記為第一層,第二層,第三層…第n層… 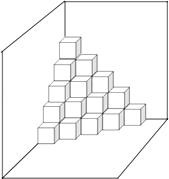
(1)第三層有個小正方體.
(2)從第四層至第六層(含第四層和第六層)共有個小正方體.
(3)第n層有個小正方體.
(4)若每個小正方體邊長為a分米,共擺放了n層,則要將擺放的小正方體能看到的表面部分涂上防銹漆,則防銹漆的總面積為分米2 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com