
【題目】已知二次函數(shù) ![]() 的圖象開口向上,與 x軸的交點(diǎn)坐標(biāo)是(1,0),對(duì)稱軸x=-1.下列結(jié)論中,錯(cuò)誤的是( )
的圖象開口向上,與 x軸的交點(diǎn)坐標(biāo)是(1,0),對(duì)稱軸x=-1.下列結(jié)論中,錯(cuò)誤的是( )
A.abc<0
B.b=2a
C.a+b+c=0
D.2 ![]()
【答案】D
【解析】由已知可得,拋物線開口向上,則 ![]() ;對(duì)稱軸是x=-1<0,則
;對(duì)稱軸是x=-1<0,則 ![]() ;又與x軸的交點(diǎn)坐標(biāo)是(1,0),則與x軸的另一個(gè)交點(diǎn)是(-3,0),因此與y軸交于負(fù)半軸,所以
;又與x軸的交點(diǎn)坐標(biāo)是(1,0),則與x軸的另一個(gè)交點(diǎn)是(-3,0),因此與y軸交于負(fù)半軸,所以 ![]() 。因此
。因此 ![]() ,故A選項(xiàng)正確
,故A選項(xiàng)正確
對(duì)稱軸是 ![]() ,則
,則 ![]() ,故B選項(xiàng)正確
,故B選項(xiàng)正確
與與x軸的交點(diǎn)坐標(biāo)是(1,0),即當(dāng) ![]() 時(shí),
時(shí), ![]() 。即
。即 ![]() ,故C選項(xiàng)正確
,故C選項(xiàng)正確
由B選項(xiàng)可知, ![]() ,故D選項(xiàng)錯(cuò)誤
,故D選項(xiàng)錯(cuò)誤
故答案為:D
拋物線開口向上,可得出a > 0,對(duì)稱軸是x=-1,又與x軸的交點(diǎn)坐標(biāo)是(1,0),則與x軸的另一個(gè)交點(diǎn)橫坐標(biāo)x可利用對(duì)稱性,中點(diǎn)公式,1-(-1)=(-1)-x,x=-3,與y軸交于負(fù)半軸可得 c < 0,a+b+c的值就是x=1時(shí)的函數(shù)值,由已知得與x軸的交點(diǎn)坐標(biāo)是(1,0), a + b + c = 0.


 天天練口算系列答案
天天練口算系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知函數(shù)y=ax2+bx+c ![]() 的圖象如圖所示,有以下四個(gè)結(jié)論:①abc=0,②
的圖象如圖所示,有以下四個(gè)結(jié)論:①abc=0,② ![]() ,③
,③ ![]() ,④
,④ ![]() ;其中正確的結(jié)論有( )
;其中正確的結(jié)論有( )
A.1個(gè)
B.2個(gè)
C.3個(gè)
D.4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,有一圓錐形糧堆,其側(cè)面展開圖是半徑為6m的半圓,糧堆母線AC的中點(diǎn)P處有一老鼠正在偷吃糧食,此時(shí),小貓正在B處,它要沿圓錐側(cè)面到達(dá)P處捕捉老鼠,則小貓所經(jīng)過的最短路程長(zhǎng)為( )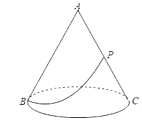
A.3m
B.![]() m
m
C.![]() m
m
D.4m
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,將△ABC沿直線MN翻折后,頂點(diǎn)C恰好落在AB邊上的點(diǎn)D處,已知MN∥AB,MC=6,NC= ![]() ,則四邊形MABN的面積是( )
,則四邊形MABN的面積是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中點(diǎn),E是AD的中點(diǎn).過點(diǎn)A作AF∥BC交BE的延長(zhǎng)線于點(diǎn)F.
,D是BC的中點(diǎn),E是AD的中點(diǎn).過點(diǎn)A作AF∥BC交BE的延長(zhǎng)線于點(diǎn)F.

(1)求證:△AEF≌△DEB;
(2)證明四邊形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,反比例函數(shù) ![]() 的圖象與一次函數(shù)y=x+b的圖象交于點(diǎn)A(1,4)、點(diǎn)B(-4,n).
的圖象與一次函數(shù)y=x+b的圖象交于點(diǎn)A(1,4)、點(diǎn)B(-4,n).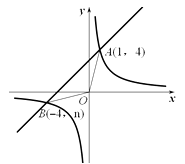
(1)求△OAB的面積;
(2)根據(jù)圖象,直接寫出不等式 ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,一動(dòng)點(diǎn)從半徑為2的⊙O上的A0點(diǎn)出發(fā),沿著射線A0O方向運(yùn)動(dòng)到⊙O上的點(diǎn)A1處,再向左沿著與射線A1O夾角為60°的方向運(yùn)動(dòng)到⊙O上的點(diǎn)A2處;接著又從A2點(diǎn)出發(fā),沿著射線A2O方向運(yùn)動(dòng)到⊙O上的點(diǎn)A3處,再向左沿著與射線A3O夾角為60°的方向運(yùn)動(dòng)到⊙O上的點(diǎn)A4處;…按此規(guī)律運(yùn)動(dòng)到點(diǎn)A2017處,則點(diǎn)A2017與點(diǎn)A0間的距離是( )
A.4
B.2 ![]()
C.2
D.0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,在矩形![]() 中,
中,![]() 的平分線DE交BC邊于點(diǎn)E,點(diǎn)P在線段DE上(其中EP<PD).
的平分線DE交BC邊于點(diǎn)E,點(diǎn)P在線段DE上(其中EP<PD).
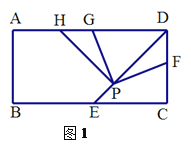
(1)如圖1,若點(diǎn)F在CD邊上(不與點(diǎn)C,D重合),將![]() 繞點(diǎn)P逆時(shí)針旋轉(zhuǎn)90°后,角的兩邊PD、PF分別交AD邊于點(diǎn)H、G.
繞點(diǎn)P逆時(shí)針旋轉(zhuǎn)90°后,角的兩邊PD、PF分別交AD邊于點(diǎn)H、G.
①求證:![]() ;
;
②探究:![]() 、
、![]() 、
、![]() 之間有怎樣的數(shù)量關(guān)系,并證明你的結(jié)論;
之間有怎樣的數(shù)量關(guān)系,并證明你的結(jié)論;
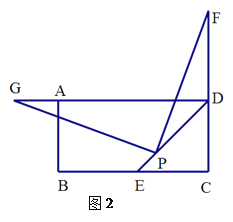
(2)拓展:如圖2,若點(diǎn)F在CD的延長(zhǎng)線上,過點(diǎn)P作![]() ,交射線DA于點(diǎn)G.你認(rèn)為(2)中DF、DG、DP之間的數(shù)量關(guān)系是否仍然成立?若成立,給出證明,若不成立,請(qǐng)寫出它們所滿足的數(shù)量關(guān)系式,并說明理由.
,交射線DA于點(diǎn)G.你認(rèn)為(2)中DF、DG、DP之間的數(shù)量關(guān)系是否仍然成立?若成立,給出證明,若不成立,請(qǐng)寫出它們所滿足的數(shù)量關(guān)系式,并說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com