
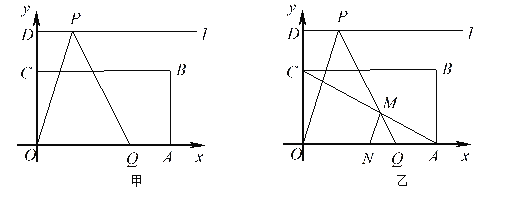
【題目】如圖(13),矩形![]() 中,
中,![]() 、
、![]() 、
、![]() ,射線
,射線![]() 過點
過點![]() 且與
且與![]() 軸平行,點
軸平行,點![]() 、
、![]() 分別是
分別是![]() 和
和![]() 軸正半軸上動點,滿足
軸正半軸上動點,滿足![]() .
.
(1)①點![]() 的坐標是 ;②
的坐標是 ;②![]() = 度;③當點
= 度;③當點![]() 與點
與點![]() 重合時,點
重合時,點![]() 的坐標為 ;
的坐標為 ;
(2)設![]() 的中點為
的中點為![]() ,
,![]() 與線段
與線段![]() 相交于點
相交于點![]() ,連結
,連結![]() ,如圖(13)乙所示,若
,如圖(13)乙所示,若![]() 為等腰三角形,求點
為等腰三角形,求點![]() 的橫坐標;
的橫坐標;
(3)設點![]() 的橫坐標為
的橫坐標為![]() ,且
,且![]() ,
,![]() 與矩形
與矩形![]() 的重疊部分的面積為
的重疊部分的面積為![]() ,試求
,試求![]() 與
與![]() 的函數關系式.
的函數關系式.
【答案】(1)(![]() ,
,![]() );
);![]() ;(
;(![]() ,
,![]() );(2)點P的橫坐標為m=0或
);(2)點P的橫坐標為m=0或![]() 或
或![]() .(3)見解析.
.(3)見解析.
【解析】分析:(1)、①由四邊形OABC是矩形,根據矩形的性質,即可求得點B的坐標:②由正切函數,即可求得∠CAO的度數:③由三角函數的性質,即可求得點P的坐標;(2)、設點![]() 的橫坐標為
的橫坐標為![]() ,分別根據MN=AN=3,AM=AN和AM=MN三種情況分別求出m的值;(3)、分別從當0≤x≤3時,當3<x≤5時,當5<x≤9時,當x>9時去分析求解即可求得答案.
,分別根據MN=AN=3,AM=AN和AM=MN三種情況分別求出m的值;(3)、分別從當0≤x≤3時,當3<x≤5時,當5<x≤9時,當x>9時去分析求解即可求得答案.
詳解:(1)、(![]() ,
,![]() );
);![]() ;(
;(![]() ,
,![]() )
)
(2)、設點![]() 的橫坐標為
的橫坐標為![]() ,
,
①當![]() ,則
,則![]() ,∴
,∴![]() ,
,
∵![]() ,∴點
,∴點![]() 與
與![]() 重合,點
重合,點![]() 與
與![]() 重合,∴
重合,∴![]() ;
;
②當![]() ,作
,作![]() 軸、
軸、![]() 軸,
軸,![]() =
=![]() ,
,
又![]() ,∴
,∴![]() ,解得:m=3﹣
,解得:m=3﹣![]() ;
;
③當![]() ,此時
,此時![]() 點的橫坐標為
點的橫坐標為![]() ,過點
,過點![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,過
,過![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ;
;
綜上所述,點![]() 的橫坐標為
的橫坐標為![]() 或
或![]() 或
或![]() ;
;
(3)、當0≤x≤3時,如圖1,OI=x,IQ=PItan60°=3,OQ=OI+IQ=3+x;
由題意可知直線l∥BC∥OA, 可得![]() ,∴EF=
,∴EF=![]() (3+x),
(3+x),
此時重疊部分是梯形,其面積為:
![]() ;
;
當3<x≤5時,如圖2,

當5<x≤9時,如圖3,

當x>9時,如圖4,![]() 。
。
綜上所述,S與x的函數關系式為:  。
。








科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
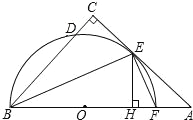
(1)求證:AC是⊙O的切線.
(2)過點E作EH⊥AB于點H,求證:CD=HF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛運用本學期的知識,設計了一個數學探究活動.如圖1,數軸上的點![]() ,
,![]() 所表示的數分別為0,12.將一枚棋子放置在點
所表示的數分別為0,12.將一枚棋子放置在點![]() 處,讓這枚棋子沿數軸在線段
處,讓這枚棋子沿數軸在線段![]() 上往復運動(即棋子從點
上往復運動(即棋子從點![]() 出發沿數軸向右運動,當運動到點
出發沿數軸向右運動,當運動到點![]() 處,隨即沿數軸向左運動,當運動到點
處,隨即沿數軸向左運動,當運動到點![]() 處,隨即沿數軸向右運動,如此反復).并且規定棋子按照如下的步驟運動:第1步,從點
處,隨即沿數軸向右運動,如此反復).并且規定棋子按照如下的步驟運動:第1步,從點![]() 開始運動
開始運動![]() 個單位長度至點
個單位長度至點![]() 處;第2步,從點
處;第2步,從點![]() 繼續運動
繼續運動![]() 單位長度至點
單位長度至點![]() 處;第3步,從點
處;第3步,從點![]() 繼續運動
繼續運動![]() 個單位長度至點
個單位長度至點![]() 處…例如:當
處…例如:當![]() 時,點
時,點![]() 、
、![]() 、
、![]() 的位置如圖2所示.
的位置如圖2所示.
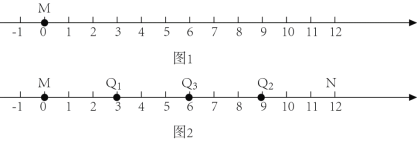
解決如下問題:
(1)如果![]() ,那么線段
,那么線段![]() ______;
______;
(2)如果![]() ,且點
,且點![]() 表示的數為3,那么
表示的數為3,那么![]() ______;
______;
(3)如果![]() ,且線段
,且線段![]() ,那么請你求出
,那么請你求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為打造書香校園,計劃購進甲、乙兩種規格的書柜放置新購進的圖書,調查發現,若購買甲種書柜3個、乙種書柜2個,共需資金1020元;若購買甲種書柜4個,乙種書柜3個,共需資金1440元.
(1)甲、乙兩種書柜每個的價格分別是多少元?
(2)若該校計劃購進這兩種規格的書柜共20個,其中乙種書柜的數量不少于甲種書柜的數量,學校至多能夠提供資金4320元,請設計幾種購買方案供這個學校選擇.
查看答案和解析>>
科目:初中數學 來源: 題型:
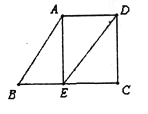
【題目】如圖,已知AB∥DE,∠B=60°,AE⊥BC,垂足為點E.
(1)求∠AED的度數;
(2)當∠EDC滿足什么條件時,AE∥DC,證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]() ,則下列結論中正確的是( )
,則下列結論中正確的是( )
①當a=5時,方程組的解是![]() ;
;
②當x,y的值互為相反數時,a=20;
③不存在一個實數a使得x=y;
④若![]() ,則a=2.
,則a=2.
A. ①②③④ B. ②③ C. ②③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司為了了解員工每人所創年利潤情況,公司從各部抽取部分員工對每年所創利潤進行統計,并繪制如圖1,圖2統計圖.
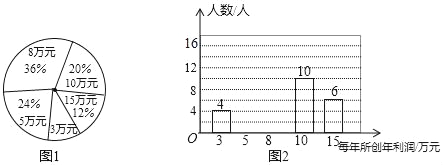
(1)將圖2補充完整;
(2)本次共抽取員工 人,每人所創年利潤的眾數是 萬元,平均數是 萬元,中位數是 萬元;
(3)若每人創造年利潤10萬元及(含10萬元)以上為優秀員工,在公司1200員工中有多少可以評為優秀員工?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從以下四張圖片中隨機抽取一張,概率為 ![]() 的事件是( )
的事件是( )

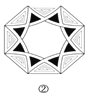


A. 是軸對稱圖形 B. 是中心對稱圖形
C. 既是軸對稱圖形又是中心對稱圖形 D. 是軸對稱圖形但不是中心對稱圖形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在Rt△ABC中,∠ACB=90°,D是邊AB的中點,BE⊥CD,垂足為點E.已知AC=15,cosA=![]() .
.
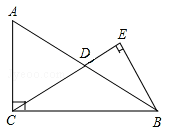
(1)求線段CD的長;
(2)求sin∠DBE的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com