
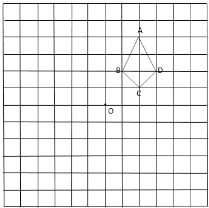
【題目】如圖,在邊長(zhǎng)為1個(gè)單位長(zhǎng)度的小正方形組成的網(wǎng)格中,已知格點(diǎn)四邊形![]() (頂點(diǎn)是網(wǎng)格線的交點(diǎn))和格點(diǎn)
(頂點(diǎn)是網(wǎng)格線的交點(diǎn))和格點(diǎn)![]() .
.
(1)將四邊形![]() 先向左平移4個(gè)單位長(zhǎng)度,再向下平移6個(gè)單位長(zhǎng)度,得到四邊形
先向左平移4個(gè)單位長(zhǎng)度,再向下平移6個(gè)單位長(zhǎng)度,得到四邊形![]() ,畫(huà)出平移后的四邊形
,畫(huà)出平移后的四邊形![]() (點(diǎn)
(點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 的對(duì)應(yīng)點(diǎn)分別為點(diǎn)
的對(duì)應(yīng)點(diǎn)分別為點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)將四邊形![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,得到四邊形
,得到四邊形![]() ,畫(huà)出旋轉(zhuǎn)后的四邊形
,畫(huà)出旋轉(zhuǎn)后的四邊形![]() (點(diǎn)
(點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 的對(duì)應(yīng)點(diǎn)分別為點(diǎn)
的對(duì)應(yīng)點(diǎn)分別為點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)填空:點(diǎn)![]() 到
到![]() 的距離為________.
的距離為________.
【答案】(1)畫(huà)圖見(jiàn)解析;(2)畫(huà)圖見(jiàn)解析,(3)![]() .
.
【解析】
(1)根據(jù)網(wǎng)格結(jié)構(gòu)找出A、B、C、D平移后的對(duì)應(yīng)點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 的位置,然后順次連接即可;
的位置,然后順次連接即可;
(2)根據(jù)網(wǎng)格結(jié)構(gòu)找出A、B、C、D繞O點(diǎn)旋轉(zhuǎn)90°后的對(duì)應(yīng)點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 的位置,然后順次連接即可;
的位置,然后順次連接即可;
(3)連接![]() ,則
,則![]() ,由勾股定理,易得
,由勾股定理,易得![]() ,再由
,再由![]() ,即可求出點(diǎn)
,即可求出點(diǎn)![]() 到
到![]() 的距離.
的距離.
(1)如圖,四邊形![]() 即為所求.
即為所求.
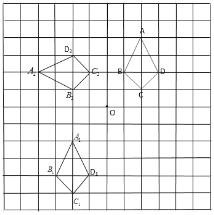
(2)如圖,四邊形![]() 即為所求.
即為所求.
(3)![]()
如圖連接![]() ,
,
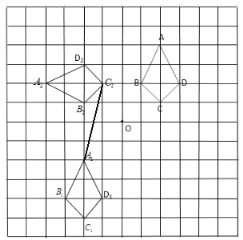
則![]() .由勾股定理,易得
.由勾股定理,易得![]() ,點(diǎn)
,點(diǎn)![]() 到
到![]() 的距離為
的距離為![]() .
.


 快捷英語(yǔ)周周練系列答案
快捷英語(yǔ)周周練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AB=AC=10cm,BD⊥AC于點(diǎn)D,BD=8cm.點(diǎn)M從點(diǎn)A出發(fā),沿AC的方向勻速運(yùn)動(dòng),同時(shí)直線PQ由點(diǎn)B出發(fā),沿BA的方向勻速運(yùn)動(dòng),運(yùn)動(dòng)過(guò)程中始終保持PQ∥AC,直線PQ交AB于點(diǎn)P、交BC于點(diǎn)Q、交BD于點(diǎn)F.連接PM,設(shè)運(yùn)動(dòng)時(shí)間為t秒(0<t≤5).線段CM的長(zhǎng)度記作y甲,線段BP的長(zhǎng)度記作y乙,y甲和y乙關(guān)于時(shí)間t的函數(shù)變化情況如圖所示.
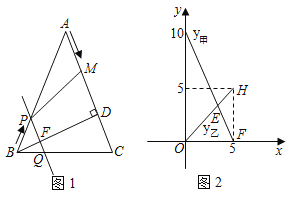
(1)由圖2可知,點(diǎn)M的運(yùn)動(dòng)速度是每秒 cm;當(dāng)t= 秒時(shí),四邊形PQCM是平行四邊形?在圖2中反映這一情況的點(diǎn)是 (并寫(xiě)出此點(diǎn)的坐標(biāo));
(2)設(shè)四邊形PQCM的面積為ycm2,求y與t之間的函數(shù)關(guān)系式;
(3)連接PC,是否存在某一時(shí)刻t,使點(diǎn)M在線段PC的垂直平分線上?若存在,求出此時(shí)t的值;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
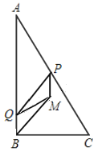
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點(diǎn)
.點(diǎn)![]() 在
在![]() 上以每秒
上以每秒![]() 個(gè)單位長(zhǎng)度的速度向終點(diǎn)
個(gè)單位長(zhǎng)度的速度向終點(diǎn)![]() 運(yùn)動(dòng).點(diǎn)
運(yùn)動(dòng).點(diǎn)![]() 沿
沿![]() 方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng),當(dāng)點(diǎn)
方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng),當(dāng)點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合時(shí),連結(jié)
重合時(shí),連結(jié)![]() ,以
,以![]() ,
,![]() 為鄰邊作
為鄰邊作![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 停止運(yùn)動(dòng)時(shí),點(diǎn)
停止運(yùn)動(dòng)時(shí),點(diǎn)![]() 也隨之停止運(yùn)動(dòng),設(shè)點(diǎn)
也隨之停止運(yùn)動(dòng),設(shè)點(diǎn)![]() 的運(yùn)動(dòng)時(shí)間為
的運(yùn)動(dòng)時(shí)間為![]() ,
,![]() 與
與![]() 重疊部分的圖形面積為
重疊部分的圖形面積為![]() .
.
(1)點(diǎn)![]() 到邊
到邊![]() 的距離
的距離![]() ,點(diǎn)
,點(diǎn)![]() 到邊
到邊![]() 的距離
的距離![]() ;(用含
;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)當(dāng)點(diǎn)![]() 落在線段
落在線段![]() 上時(shí),求
上時(shí),求![]() 的值;
的值;
(3)求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(4)連結(jié)![]() ,當(dāng)
,當(dāng)![]() 與
與![]() 的一邊平行或垂直時(shí),直接寫(xiě)出
的一邊平行或垂直時(shí),直接寫(xiě)出![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)的運(yùn)動(dòng)服裝專柜,對(duì)![]() 兩種品牌的遠(yuǎn)動(dòng)服分兩次采購(gòu)試銷后,效益可觀,計(jì)劃繼續(xù)采購(gòu)進(jìn)行銷售.已知這兩種服裝過(guò)去兩次的進(jìn)貨情況如下表.
兩種品牌的遠(yuǎn)動(dòng)服分兩次采購(gòu)試銷后,效益可觀,計(jì)劃繼續(xù)采購(gòu)進(jìn)行銷售.已知這兩種服裝過(guò)去兩次的進(jìn)貨情況如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累計(jì)采購(gòu)款/元 | 10200 | 14400 |
(1)問(wèn)![]() 兩種品牌運(yùn)動(dòng)服的進(jìn)貨單價(jià)各是多少元?
兩種品牌運(yùn)動(dòng)服的進(jìn)貨單價(jià)各是多少元?
(2)由于![]() 品牌運(yùn)動(dòng)服的銷量明顯好于
品牌運(yùn)動(dòng)服的銷量明顯好于![]() 品牌,商家決定采購(gòu)
品牌,商家決定采購(gòu)![]() 品牌的件數(shù)比
品牌的件數(shù)比![]() 品牌件數(shù)的
品牌件數(shù)的![]() 倍多5件,在采購(gòu)總價(jià)不超過(guò)21300元的情況下,最多能購(gòu)進(jìn)多少件
倍多5件,在采購(gòu)總價(jià)不超過(guò)21300元的情況下,最多能購(gòu)進(jìn)多少件![]() 品牌運(yùn)動(dòng)服?
品牌運(yùn)動(dòng)服?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 是
是![]() 邊的中點(diǎn),
邊的中點(diǎn),![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,連接
,連接![]() .則列四個(gè)結(jié)論:
.則列四個(gè)結(jié)論:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結(jié)論有:
.其中正確的結(jié)論有:
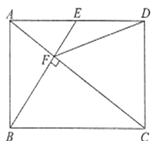
A.4個(gè)B.3個(gè)C.2個(gè)D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】關(guān)于二次函數(shù)y=2x2﹣mx+m﹣2,以下結(jié)論:
①拋物線交x軸有交點(diǎn);
②不論m取何值,拋物線總經(jīng)過(guò)點(diǎn)(1,0);
③若m>6,拋物線交x軸于A、B兩點(diǎn),則AB>1;
④拋物線的頂點(diǎn)在y=﹣2(x﹣1)2圖象上.其中正確的序號(hào)是( )
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,要設(shè)計(jì)一幅寬20厘米,長(zhǎng)30厘米的圖案,其中有兩橫兩豎的彩條,橫、豎彩條的寬度比為2∶1,如果要使彩條所占面積是圖案面積的一半,那么豎彩條寬度是多少?若設(shè)豎彩條寬度是x厘米,則根據(jù)題意可列方程_____________.
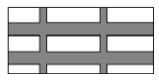
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
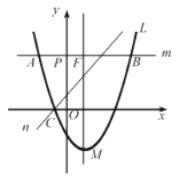
【題目】如圖,拋物線![]() (
(![]() ,
,![]() 為常數(shù)且
為常數(shù)且![]() )經(jīng)過(guò)點(diǎn)
)經(jīng)過(guò)點(diǎn)![]() ,頂點(diǎn)為
,頂點(diǎn)為![]() ,經(jīng)過(guò)點(diǎn)
,經(jīng)過(guò)點(diǎn)![]() 的直線
的直線![]() 與
與![]() 軸平行,且
軸平行,且![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() (
(![]() 在
在![]() 的右側(cè)),與
的右側(cè)),與![]() 的對(duì)稱軸交于點(diǎn)
的對(duì)稱軸交于點(diǎn)![]() ,直線
,直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() .
.
(1)用![]() 表示
表示![]() 及點(diǎn)
及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)![]() 的值是否是定值?若是,請(qǐng)求出這個(gè)定值;若不是,請(qǐng)說(shuō)明理由;
的值是否是定值?若是,請(qǐng)求出這個(gè)定值;若不是,請(qǐng)說(shuō)明理由;
(3)當(dāng)直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() 時(shí),求
時(shí),求![]() 的值及點(diǎn)
的值及點(diǎn)![]() ,
,![]() 的坐標(biāo);
的坐標(biāo);
(4)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 的外心為點(diǎn)
的外心為點(diǎn)![]() ,則
,則
①求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②若點(diǎn)![]() 在
在![]() 的對(duì)稱軸上,其縱坐標(biāo)為
的對(duì)稱軸上,其縱坐標(biāo)為![]() ,且滿足
,且滿足![]() ,直接寫(xiě)出
,直接寫(xiě)出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
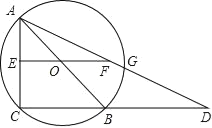
【題目】如圖,已知AB是⊙O的直徑,C是⊙O上的點(diǎn),連接AC、CB,過(guò)O作EO∥CB并延長(zhǎng)EO到F,使EO=FO,連接AF并延長(zhǎng),AF與CB的延長(zhǎng)線交于D.求證:AE2=FGFD.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com