
【題目】定義:有一組鄰邊相等的凸四邊形叫做“準(zhǔn)菱形”.利用該定義完成以下各題:
(1) 理解
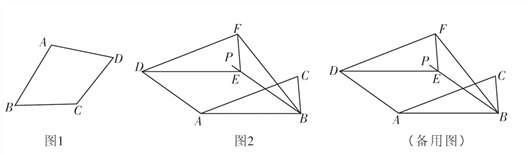
填空:如圖1,在四邊形ABCD中,若 (填一種情況),則四邊形ABCD是“準(zhǔn)菱形”;
(2)應(yīng)用
證明:對角線相等且互相平分的“準(zhǔn)菱形”是正方形;(請畫出圖形,寫出已知,求證并證明)
(3) 拓展
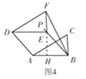
如圖2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,將Rt△ABC沿∠ABC的平分線BP方向平移得到△DEF,連接AD,BF,若平移后的四邊形ABFD是“準(zhǔn)菱形”,求線段BE的長.
【答案】(1)答案不唯一,如AB=BC.(2)見解析;(3) BE=2或![]() 或
或![]() 或
或![]() .
.
【解析】整體分析:
(1)根據(jù)“準(zhǔn)菱形”的定義解答,答案不唯一;(2)對角線相等且互相平分的四邊形是矩形,矩形的鄰邊相等時即是正方形;(3)根據(jù)平移的性質(zhì)和“準(zhǔn)菱形”的定義,分四種情況畫出圖形,結(jié)合勾股定理求解.
解:(1)答案不唯一,如AB=BC.
(2)已知:四邊形ABCD是“準(zhǔn)菱形”,AB=BC,對角線AC,BO交于點(diǎn)O,且AC=BD,OA=OC,OB=OD.
求證:四邊形ABCD是正方形.
證明:∵OA=OC,OB=OD,
∴四邊形ABCD是平行四邊形.
∵AC=BD,
∴平行四邊形ABCD是矩形.
∵四邊形ABCD是“準(zhǔn)菱形”,AB=BC,
∴四邊形ABCD是正方形.
(3)由平移得BE=AD,DE=AB=2,EF=BC=1,DF=AC=![]() .
.
由“準(zhǔn)菱形”的定義有四種情況:
①如圖1,當(dāng)AD=AB時,BE=AD=AB=2.
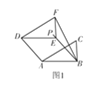
②如圖2,當(dāng)AD=DF時,BE=AD=DF=![]() .
.
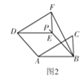
③如圖3,當(dāng)BF=DF=![]() 時,延長FE交AB于點(diǎn)H,則FH⊥AB.
時,延長FE交AB于點(diǎn)H,則FH⊥AB.
∵BE平分∠ABC,∴∠ABE=![]() ∠ABC=45°.
∠ABC=45°.
∴∠BEH=∠ABE=45°.∴BE=![]() BH.
BH.
設(shè)EH=BH=x,則FH=x+1,BE=![]() x.
x.
∵在Rt△BFH中,BH2+FH2=BF2,
∴x2+(x+1)2=(![]() )2,
)2,
解得x1=1,x2=-2(不合題意,舍去),
∴BE=![]() x=
x=![]() .
.
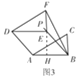
④如圖4,當(dāng)BF=AB=2時,與③)同理得:BH2+FH2=BF2.
設(shè)EH=BH=x,則x2+(x+1)2=22,
解得x1=![]() ,x2=
,x2=![]() (不合題意,舍去),
(不合題意,舍去),
∴BE=![]() x=
x=![]() .
.
綜上所述,BE=2或![]() 或
或![]() 或
或![]() .
.


 小學(xué)生10分鐘口算測試100分系列答案
小學(xué)生10分鐘口算測試100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
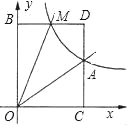
【題目】如圖,已知正比例函數(shù)y=ax與反比例函數(shù)y=![]() 的圖象交于點(diǎn)A(3,2)
的圖象交于點(diǎn)A(3,2)
(1)求上述兩函數(shù)的表達(dá)式;
(2)M(m,n)是反比例函數(shù)圖象上的一個動點(diǎn),其中0<m<3,過點(diǎn)M作直線MB∥x軸,交y軸于點(diǎn)B;過點(diǎn)A點(diǎn)作直線AC∥y軸交x軸于點(diǎn)C,交直線MB于點(diǎn)D.若s四邊形OADM=6,求點(diǎn)M的坐標(biāo),并判斷線段BM與DM的大小關(guān)系,說明理由;
(3)探索:x軸上是否存在點(diǎn)P.使△OAP是等腰三角形?若存在,求出點(diǎn)P的坐標(biāo); 若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在數(shù)軸上![]() 點(diǎn)表示數(shù)
點(diǎn)表示數(shù)![]() ,
,![]() 點(diǎn)表示數(shù)
點(diǎn)表示數(shù)![]() ,
,![]() 滿足
滿足![]()
![]()
(1)點(diǎn)![]() 表示的數(shù)為 ,點(diǎn)
表示的數(shù)為 ,點(diǎn)![]() 表示的數(shù)為 .
表示的數(shù)為 .
(2)若點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 之間的距離表示為
之間的距離表示為![]() ,點(diǎn)
,點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 之間的距離表示為
之間的距離表示為![]() ,請?jiān)跀?shù)軸上找一點(diǎn)
,請?jiān)跀?shù)軸上找一點(diǎn)![]() ,使
,使![]() ,則
,則![]() 表示的數(shù)為 .
表示的數(shù)為 .
(3)如圖,若在原點(diǎn)![]() 處放一擋板,一小球甲從點(diǎn)
處放一擋板,一小球甲從點(diǎn)![]() 處以1個單位/秒的速度向左運(yùn)動;同時另一小球乙從點(diǎn)
處以1個單位/秒的速度向左運(yùn)動;同時另一小球乙從點(diǎn)![]() 處以2單位/秒的速度也向左運(yùn)動,在碰到擋板后(忽略球的大小,可看作一點(diǎn))以原來的速度向相反的方向運(yùn)動,設(shè)運(yùn)動的時間為
處以2單位/秒的速度也向左運(yùn)動,在碰到擋板后(忽略球的大小,可看作一點(diǎn))以原來的速度向相反的方向運(yùn)動,設(shè)運(yùn)動的時間為![]() (秒),
(秒),
![]()
①分別表示出甲、乙兩小球到原點(diǎn)的距離(用![]() 表示);
表示);
②求甲、乙兩小球到原點(diǎn)的距離相等時經(jīng)歷的時間.
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某品牌飲水機(jī)廠生產(chǎn)一種飲水機(jī)和飲水機(jī)桶,飲水機(jī)每臺定價(jià)350元,飲水機(jī)桶每只定價(jià)50元,廠方開展促銷活動期間,可以同時向客戶提供兩種優(yōu)惠方案:
方案一:買一臺飲水機(jī)送一只飲水機(jī)桶;
方案二:飲水機(jī)和飲水機(jī)桶都按定價(jià)的90%付款.
現(xiàn)某客戶到該飲水機(jī)廠購買飲水機(jī)30臺,飲水機(jī)桶![]() 只(
只(![]() 超過30).
超過30).
(1)若該客戶按方案一購買,求客戶需付款(用含![]() 的式子表示);若該客戶按方案二購買,求客戶需付款(用含
的式子表示);若該客戶按方案二購買,求客戶需付款(用含![]() 的式子表示);
的式子表示);
(2)若![]() 時,通過計(jì)算說明此時按哪種方案購買較為合算?
時,通過計(jì)算說明此時按哪種方案購買較為合算?
(3)當(dāng)![]() 時,你能給出一種更為省錢的購買方案嗎?試寫出你的購買方法,并計(jì)算出所需的錢數(shù).
時,你能給出一種更為省錢的購買方案嗎?試寫出你的購買方法,并計(jì)算出所需的錢數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
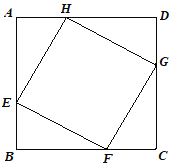
【題目】如圖,正方形ABCD的邊長為8cm,E、F、G、H分別是AB、BC、CD、DA上的動點(diǎn),且AE=BF=CG=DH.則四邊形EFGH面積的最小值是________cm2.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
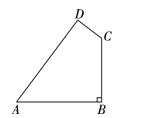
【題目】如圖,某開發(fā)區(qū)有一塊四邊形空地ABCD,現(xiàn)計(jì)劃在空地上種植草皮,經(jīng)測量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,則種植這片草皮需要多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】做大小兩個長方體紙盒,尺寸如下(單位:cm)
長 | 寬 | 高 | |
小紙盒 |
|
|
|
大紙盒 |
|
|
|
(1) 做這兩個紙盒共用料多少![]() ?
?
(2) 做小紙盒比做大紙盒少用料多少![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
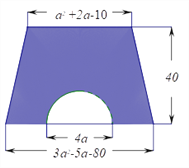
【題目】如圖,梯形的上底為![]() +2
+2![]() -10,下底為3
-10,下底為3![]() -5
-5![]() -80,高為40.(
-80,高為40.(![]() 取3)
取3)
(1)用式子表示圖中陰影部分的面積;
(2)當(dāng)![]() =10時,求陰影部分面積的值。
=10時,求陰影部分面積的值。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com