
【題目】已知在平面直角坐標中,點A(m,n)在第一象限內(nèi),AB⊥OA且AB=OA,反比例函數(shù)y=![]() 的圖象經(jīng)過點A,
的圖象經(jīng)過點A,
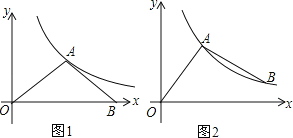
(1)當點B的坐標為(4,0)時(如圖1),求這個反比例函數(shù)的解析式;
(2)當點B在反比例函數(shù)y=![]() 的圖象上,且在點A的右側(cè)時(如圖2),用含字母m,n的代數(shù)式表示點B的坐標;
的圖象上,且在點A的右側(cè)時(如圖2),用含字母m,n的代數(shù)式表示點B的坐標;
(3)在第(2)小題的條件下,求![]() 的值.
的值.
【答案】(1)y=![]() ;(2)B(m+n,n﹣m);(3)
;(2)B(m+n,n﹣m);(3)![]()
【解析】
(1)根據(jù)等腰直角三角形性質(zhì),直角三角形斜邊中線定理,三線合一,得到點![]() 坐標,代入解析式即可得到
坐標,代入解析式即可得到![]() .
.
(2)過點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,過點
,過點![]() 作垂直于
作垂直于![]() 軸的直線交
軸的直線交![]() 于點
于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,構造一線三等角全等,得到
,構造一線三等角全等,得到![]() ,
,![]() ,所以
,所以![]()
(3)把點![]() 和點
和點![]() 的坐標代入反比例函數(shù)解析式得到關于
的坐標代入反比例函數(shù)解析式得到關于![]() 、
、![]() 的等式,兩邊除以
的等式,兩邊除以![]() ,換元法解得
,換元法解得![]() 的值是
的值是![]()
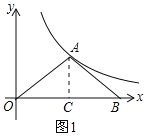
解:(1)過![]() 作
作![]() ,交
,交![]() 軸于點
軸于點![]() ,
,
![]() ,
,![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形,
![]() ,
,
![]() ,
,
將![]() ,
,![]() 代入反比例解析式得:
代入反比例解析式得:![]() ,即
,即![]() ,
,
則反比例解析式為![]() ;
;
(2)過![]() 作
作![]() 軸,過
軸,過![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
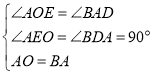 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
則![]() ;
;
(3)由![]() 與
與![]() 都在反比例圖象上,得到
都在反比例圖象上,得到![]() ,
,
整理得:![]() ,即
,即![]() ,
,
這里![]() ,
,![]() ,
,![]() ,
,
![]() △
△![]() ,
,
![]()
![]() ,
,
![]() 在第一象限,
在第一象限,
![]() ,
,![]() ,
,
則![]() .
.


科目:初中數(shù)學 來源: 題型:
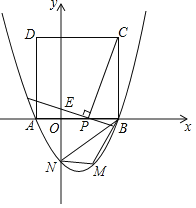
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,以
,以![]() 為邊在
為邊在![]() 軸上方作正方形
軸上方作正方形![]() ,點
,點![]() 是
是![]() 軸上一動點,連接
軸上一動點,連接![]() ,過點
,過點![]() 作
作![]() 的垂線與
的垂線與![]() 軸交于點
軸交于點![]() .
.
(1)求該拋物線的函數(shù)關系表達式;
(2)當點![]() 在線段
在線段![]() (點
(點![]() 不與
不與![]() 重合)上運動至何處時,線段
重合)上運動至何處時,線段![]() 的長有最大值?并求出這個最大值;
的長有最大值?并求出這個最大值;
(3)在第四象限的拋物線上任取一點![]() ,連接
,連接![]() .請問:
.請問:![]() 的面積是否存在最大值?若存在,求出此時點
的面積是否存在最大值?若存在,求出此時點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
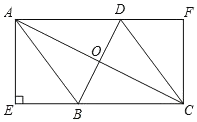
【題目】如圖,在菱形ABCD中,對角線AC,BD交于點O,AE⊥BC交CB延長線于E,CF∥AE交AD延長線于點F.
(1)求證:四邊形AECF是矩形;
(2)連接OE,若AE=8,AD=10,求OE的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,折疊矩形![]() 的一邊
的一邊![]() ,使點
,使點![]() 落在
落在![]() 邊的點
邊的點![]() 處,折痕為
處,折痕為![]() ,連接
,連接![]() .已知點
.已知點![]() 的坐標為
的坐標為![]() ,二次函數(shù)
,二次函數(shù)![]() 圖象經(jīng)過
圖象經(jīng)過![]() 、
、![]() 、
、![]() 三點.
三點.
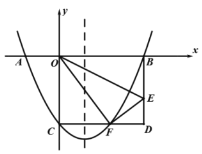
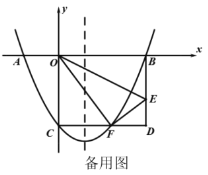
(1)求函數(shù)解析式;
(2)在![]() 軸下方拋物線上有一動點
軸下方拋物線上有一動點![]() ,過點
,過點![]() 作
作![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,連接
,連接![]() ,當
,當![]() 與
與![]() 相似時,求點
相似時,求點![]() 的坐標.
的坐標.
(3)在拋物線對稱軸上是否存在一點![]() ,使
,使![]() 有最大值?若存在,請直接寫出
有最大值?若存在,請直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知![]() 是
是![]() 的直徑,
的直徑,![]() 是
是![]() 的弦.
的弦.
(1)如圖①,連接![]() ,若
,若![]() ,求
,求![]() 的大小;
的大小;
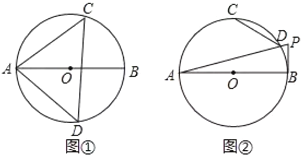
(2)如圖②;![]() 是半圓弧
是半圓弧![]() 的中點,
的中點,![]() 的延長線與過點
的延長線與過點![]() 的切線相交于點
的切線相交于點![]() ,若
,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某中學號召全校學生進行安全教育網(wǎng)絡學習,并對部分學生的學習情況進行了隨機調(diào)查.對部分學生的成績(x為整數(shù),滿分100分)進行統(tǒng)計,并繪制了如下統(tǒng)計圖表.
調(diào)查結(jié)果頻數(shù)分布表
| 調(diào)查結(jié)果扇形統(tǒng)計圖
|
根據(jù)所給信息,解答下列問題:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形統(tǒng)計圖中,m的值及A組對應的圓心角的度數(shù);
(3)若參加學習的同學共有1500人,請你估計成績不低于80分的同學有多少人.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】若一組數(shù)據(jù)1,2,3,4,x的平均數(shù)與中位數(shù)相同,則實數(shù)x的值不可能是( )
A.0B.2.5C.3D.5
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于點
與x軸交于點![]() ,點
,點![]() ,與y軸交于點C,且過點
,與y軸交于點C,且過點![]() .點P、Q是拋物線
.點P、Q是拋物線![]() 上的動點.
上的動點.
(1)求拋物線的解析式;
(2)當點P在直線OD下方時,求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點E,當![]() 與
與![]() 相似時,求點Q的坐標.
相似時,求點Q的坐標.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com