
【題目】如圖①,二次函數的拋物線的頂點坐標C,與x軸的交于A(1,0)、B(﹣3,0)兩點,與y軸交于點D(0,3).
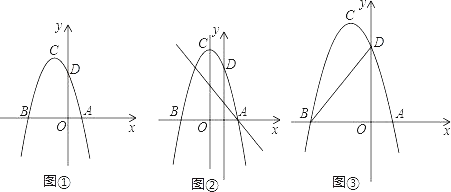
(1)求這個拋物線的解析式;
(2)如圖②,過點A的直線與拋物線交于點E,交y軸于點F,其中點E的橫坐標為﹣2,若直線PQ為拋物線的對稱軸,點G為直線PQ上的一動點,則x軸上是否存在一點H,使D、G、H、F四點所圍成的四邊形周長最小?若存在,求出這個最小值及點G、H的坐標;若不存在,請說明理由;
(3)如圖③,連接AC交y軸于M,在x軸上是否存在點P,使以P、C、M為頂點的三角形與△AOM相似?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】
【1】 設所求拋物線的解析式為:![]() ,將A(1,0)、B(-3,0)、 D(0,3)代入,得
,將A(1,0)、B(-3,0)、 D(0,3)代入,得![]() …………………………………………2分
…………………………………………2分
即所求拋物線的解析式為:![]() ……………………………3分
……………………………3分
【2】 如圖④,在y軸的負半軸上取一點I,使得點F與點I關于x軸對稱,
在x軸上取一點H,連接HF、HI、HG、GD、GE,則HF=HI…………………①
設過A、E兩點的一次函數解析式為:y=kx+b(k≠0),
∵點E在拋物線上且點E的橫坐標為-2,將x=-2,代入拋物線![]() ,得
,得![]()
∴點E坐標為(-2,3)………………………………………………………………4分
又∵拋物線![]() 圖象分別與x軸、y軸交于點A(1,0)、B(-3,0)、
圖象分別與x軸、y軸交于點A(1,0)、B(-3,0)、
D(0,3),所以頂點C(-1,4)
∴拋物線的對稱軸直線PQ為:直線x=-1, [中國教#&~@育出%版網]
∴點D與點E關于PQ對稱,GD=GE……………………………………………②
分別將點A(1,0)、點E(-2,3)
代入y=kx+b,得:
![]() 解得:
解得:![]()
過A、E兩點的一次函數解析式為:
y=-x+1
∴當x=0時,y=1
∴點F坐標為(0,1)……………………5分
∴![]() =2………………………………………③
=2………………………………………③
又∵點F與點I關于x軸對稱,
∴點I坐標為(0,-1)
∴![]() ……………………………………④
……………………………………④
又∵要使四邊形DFHG的周長最小,由于DF是一個定值,
∴只要使DG+GH+HI最小即可 ……………………………………6分
由圖形的對稱性和①、②、③,可知,
DG+GH+HF=EG+GH+HI
只有當EI為一條直線時,EG+GH+HI最小
設過E(-2,3)、I(0,-1)兩點的函數解析式為:![]() ,
,
分別將點E(-2,3)、點I(0,-1)代入![]() ,得:
,得:
![]() 解:
解:![]()
過I、E兩點的一次函數解析式為:y=-2x-1
∴當x=-1時,y=1;當y=0時,x=-![]() ;
;
∴點G坐標為(-1,1),點H坐標為(-![]() ,0)
,0)
∴四邊形DFHG的周長最小為:DF+DG+GH+HF=DF+EI
由③和④,可知:

DF+EI=![]()
∴四邊形DFHG的周長最小為![]() . …………………………………………7分
. …………………………………………7分
【3】 如圖⑤,
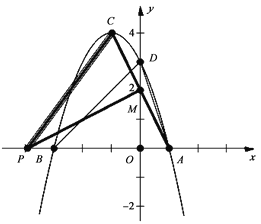
由(2)可知,點A(1,0),點C(-1,4),設過A(1,0),點C(-1,4)兩點的函數解析式為:![]() ,得:
,得:![]()
解得:![]() ,
,
過A、C兩點的一次函數解析式為:y=-2x+2,當x=0時,y=2,即M的坐標為(0,2);
由圖可知,△AOM為直角三角形,且![]() , ………………8分
, ………………8分
要使,△AOM與△PCM相似,只要使△PCM為直角三角形,且兩直角邊之比為1:2即可,設P(![]() ,0),CM=
,0),CM=![]() ,且∠CPM不可能為90°時,因此可分兩種情況討論; ……………………………………………………………………………9分
,且∠CPM不可能為90°時,因此可分兩種情況討論; ……………………………………………………………………………9分
①當∠CMP=90°時,CM=![]() ,若
,若![]() 則
則![]() ,可求的P(-4,0),則CP=5,
,可求的P(-4,0),則CP=5,![]() ,即P(-4,0)成立,若
,即P(-4,0)成立,若![]() 由圖可判斷不成立;……………………………………………………………………………………10分
由圖可判斷不成立;……………………………………………………………………………………10分
②當∠PCM=90°時,CM=![]() ,若
,若![]() 則
則![]() ,可求出
,可求出
P(-3,0),則PM=![]() ,顯然不成立,若
,顯然不成立,若![]() 則
則![]() ,更不可能成立.……11分
,更不可能成立.……11分
綜上所述,存在以P、C、M為頂點的三角形與△AOM相似,點P的坐標為(-4,0)12分
【解析】
(1)直接利用三點式求出二次函數的解析式;
(2)若四邊形DFHG的周長最小,應將邊長進行轉換,利用對稱性,要使四邊形DFHG的周長最小,由于DF是一個定值,只要使DG+GH+HI最小即可,
由圖形的對稱性和,可知,HF=HI,GD=GE,
DG+GH+HF=EG+GH+HI
只有當EI為一條直線時,EG+GH+HI最小,即
![]() ,DF+EI=
,DF+EI=![]()
即邊形DFHG的周長最小為![]() .
.
(3)要使△AOM與△PCM相似,只要使△PCM為直角三角形,且兩直角邊之比為1:2即可,設P(![]() ,0),CM=
,0),CM=![]() ,且∠CPM不可能為90°時,因此可分兩種情況討論,①當∠CMP=90°時,CM=
,且∠CPM不可能為90°時,因此可分兩種情況討論,①當∠CMP=90°時,CM=![]() ,若
,若![]() 則
則![]() ,可求的P(-4,0),則CP=5,
,可求的P(-4,0),則CP=5,![]() ,即P(-4,0)成立,若
,即P(-4,0)成立,若![]() 由圖可判斷不成立;②當∠PCM=90°時,CM=
由圖可判斷不成立;②當∠PCM=90°時,CM=![]() ,若
,若![]() 則
則![]() ,可求出P(-3,0),則PM=
,可求出P(-3,0),則PM=![]() ,顯然不成立,若
,顯然不成立,若![]() 則
則![]() ,更不可能成立. 即求出以P、C、M為頂點的三角形與△AOM相似的P的坐標(-4,0)
,更不可能成立. 即求出以P、C、M為頂點的三角形與△AOM相似的P的坐標(-4,0)


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a>0)的圖象的對稱軸為直線x=1,且(x1,y1),(x2,y2)為其圖象上的兩點,( )
A. 若x1>x2>1,則(y1-y2)+2a(x1-x2)<0
B. 若1>x1>x2,則(y1-y2)+2a(x1-x2)<0
C. 若x1>x2>1,則(y1-y2)+a(x1-x2)>0
D. 若1>x1>x2,則(y1-y2)+a(x1-x2)>0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解答問題.
面積與代數恒等式
通過學習,我們知道可以用圖1的面積來解釋公式![]() ,人們經常稱作用面積解釋代數恒等式實際上還有一些代數恒等式也可以用這種形式表示,如可用圖2表示
,人們經常稱作用面積解釋代數恒等式實際上還有一些代數恒等式也可以用這種形式表示,如可用圖2表示![]() .
.
請根據閱讀材料,解答下列問題:
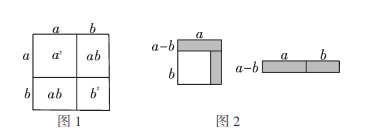
(1)請寫出圖3所表示的代數恒等式: ;
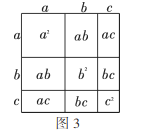
(2)試畫一個幾何圖形,使它的面積表示:![]() ;
;
(3)請仿照上述方法另寫一個含有![]() ,
,![]() 的代數恒等式,并畫出與它對應的幾何圖形.
的代數恒等式,并畫出與它對應的幾何圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
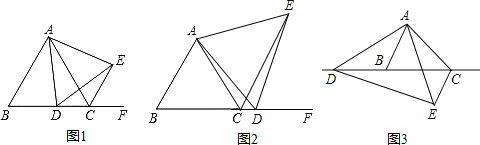
【題目】已知![]() 為等邊三角形,點
為等邊三角形,點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 、點
、點![]() 重合).連接
重合).連接![]() ,以
,以![]() 為邊向逆時針方向作等邊
為邊向逆時針方向作等邊![]() ,連接
,連接![]() ,
,
(1)如圖1,當點![]() 在邊
在邊![]() 上時:
上時:
①求證:![]() ;
;
②判斷![]() 之間的數量關系是 ;
之間的數量關系是 ;
(2)如圖2,當點![]() 在邊
在邊![]() 的延長線上時,其他條件不變,判斷
的延長線上時,其他條件不變,判斷![]() 之間存在的數量關系,并寫出證明過程;
之間存在的數量關系,并寫出證明過程;
(3)如圖3,當點![]() 在邊
在邊![]() 的反向延長線上時,其他條件不變,請直接寫出
的反向延長線上時,其他條件不變,請直接寫出![]() 之間存在的數量關系為 .
之間存在的數量關系為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y1=a1x2+b1x+c1,y2=a2x2+b2x+c2且滿足![]() (k≠0,1).則稱拋物線y1,y2互為“友好拋物線”,則下列關于 “友好拋物線”的說法不正確的是( )
(k≠0,1).則稱拋物線y1,y2互為“友好拋物線”,則下列關于 “友好拋物線”的說法不正確的是( )
A. y1,y2開口方向、開口大小不一定相同
B. 因為y1,y2的對稱軸相同
C. 如果y2的最值為m,則y1的最值為km
D. 如果y2與x軸的兩交點間距離為d,則y1與x軸的兩交點間距離為|k|d
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,CB=CD,對角線AC,BD相交于點O,下列結論中:
①∠ABC=∠ADC;
②AC與BD相互平分;
③AC,BD分別平分四邊形ABCD的兩組對角;
④四邊形ABCD的面積S=![]() ACBD.
ACBD.
正確的是 (填寫所有正確結論的序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
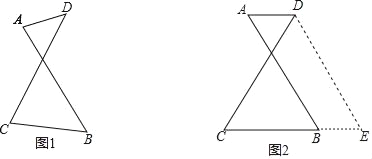
【題目】如圖1有兩條長度相等的相交線段AB、CD,它們相交的銳角中有一個角為60°,為了探究AD、CB與CD(或AB)之間的關系,小亮進行了如下嘗試:
(1)在其他條件不變的情況下使得AD∥BC,如圖2,將線段AB沿AD方向平移AD的長度,得到線段DE,然后聯結BE,進而利用所學知識得到AD、CB與CD(或AB)之間的關系: ;(直接寫出結果)
(2)根據小亮的經驗,請對圖1的情況(AD與CB不平行)進行嘗試,寫出AD、CB與CD(或AB)之間的關系,并進行證明;
(3)綜合(1)、(2)的證明結果,請寫出完整的結論: .
查看答案和解析>>
科目:初中數學 來源: 題型:
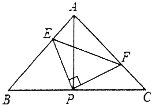
【題目】如圖,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC中點,兩邊PE、PF分別交AB、AC于點E、F,給出下列四個結論:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④![]() ,當∠EPF在△ABC內繞頂點P旋轉時(點E不與A、B重合),上述結論中始終正確的有________(把你認為正確的結論的序號都填上).
,當∠EPF在△ABC內繞頂點P旋轉時(點E不與A、B重合),上述結論中始終正確的有________(把你認為正確的結論的序號都填上).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com