【題目】如圖所示，小明家住在30米高的A樓里，小麗家住在B樓里，B樓坐落在A樓的正北面，已知當(dāng)?shù)囟林形?/span>12時太陽光線與水平面的夾角為30°．
（1）如果A、B兩樓相距16
米，那么A樓落在B樓上的影子有多長？
（2）如果A樓的影子剛好不落在B樓上，那么兩樓的距離應(yīng)是多少米？（結(jié)果保留根號）
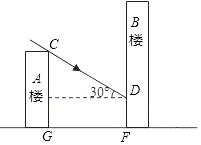
【答案】（1）A樓落在B樓上的影子有14m．（2）如果A樓的影子剛好不落在B樓上，那么兩樓的距離應(yīng)是30
米．
【解析】
（1）利用銳角三角函數(shù)關(guān)系得出CE的長，進(jìn)而得出答案；
（2）可根據(jù)A樓，地面和光線正好構(gòu)成直角三角形，利用銳角三角函數(shù)關(guān)系求解．
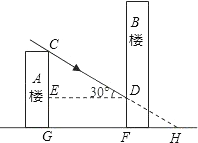
解：（1）如圖，過D作DE⊥CG于E， ED=16，∠CDE=30°，
∴CE=DEtan30°=16×
=16（m），
故DF=EG=CG-CE=30-16=14（m），
答：A樓落在B樓上的影子有14m．
（2）延長CD交GF于點H，
當(dāng)A樓的影子剛好不落在B樓上，
則GH=
=
=30（m），
答：如果A樓的影子剛好不落在B樓上，那么兩樓的距離應(yīng)是30米．
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，∠A＝∠B，AE＝BE，點D在AC邊上，∠1＝∠2，AE和BD相交于點O．
（1）求證：△AEC≌△BED；
（2）若∠1＝50°，則∠BDE＝ °．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】鄂北公司以10元/千克的價格收購一批產(chǎn)品進(jìn)行銷售，為了得到日銷售量y（千克）與銷售價格x（元/千克）之間的關(guān)系，經(jīng)過市場調(diào)查獲得部分?jǐn)?shù)據(jù)如表：
銷售價格x（元/千克） | 10 | 15 | 20 | 25 | 30 |
日銷售量y（千克） | 300 | 225 | 150 | 75 | 0 |
（1）請你根據(jù)表中的數(shù)據(jù)確定y與x之間的函數(shù)表達(dá)式；
（2）鄂北公司應(yīng)該如何確定這批產(chǎn)品的銷售價格，才能使日銷售利潤W1元最大？
（3）若鄂北公司每銷售1千克這種產(chǎn)品需支出a元（a＞0）的相關(guān)費用，當(dāng)20≤x≤25時，鄂北公司的日獲利W2元的最大值為1215元，求a的值．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】一個盒子中裝有2個紅球，1個白球和1個藍(lán)球，這些球除顏色外都相同，小明和小凡準(zhǔn)備用這些球做游戲，游戲規(guī)則如下：從盒子中隨機摸出一個球，記下顏色后放回，再從中隨機摸出一個球，若兩次摸到的球的顏色都是紅色，小明勝；若兩次摸到的球的顏色能配成紫色，則小凡勝，這個游戲?qū)﹄p方公平嗎？請說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，在矩形ABCD中，對角線AC，BD相交于點O，AB＝3cm，BC＝4cm，點E是BC上一點，且CE＝1cm．點P由點C出發(fā)，沿CD方向向點D勻速運動，速度為1cm/s；點Q由點A出發(fā)，沿AD方向向點D勻速運動，速度為
cm/s，點P，Q同時出發(fā)，PQ交BD于F，連接PE，QB，設(shè)運動時間為t(s)(0＜t＜3)．
(1)當(dāng)t為何值時，PE∥BD？
(2)設(shè)△FQD的面積為y(cm2)，求y與t之間的函數(shù)關(guān)系式．
(3)是否存在某一時刻t，使得四邊形BQPE的周長最小．若存在，求出此四邊形BQPE的面積；若不存在，請說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
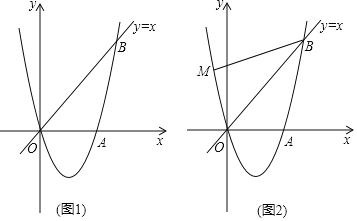
【題目】如（圖1），已知經(jīng)過原點的拋物線y＝ax2+bx與x軸交于另一點A(
，0)，在第一象限內(nèi)與直線y＝x交于點B(2，t)
（1）求拋物線的解析式；
（2）在直線OB下方的拋物線上有一點C，點C到直線OB的距離為
，求點C的坐標(biāo)；
（3）如（圖2），若點M在拋物線上，且∠MBO＝∠ABO，在（2）的條件下，是否存在點P，使得△POC∽△MOB？若存在，求出點P坐標(biāo)；若不存在，請說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
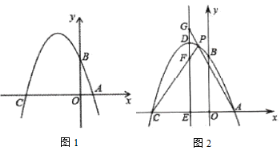
【題目】如圖1，已知在平面直角坐標(biāo)系
中，點
、
、
分別為坐標(biāo)軸上的三個點，且
，
，
．
（1）求經(jīng)過、、三點的拋物線的解析式；
（2）點
是拋物線上一個動點，且在直線
的上方，連接
、
，并把
沿
翻折，得到四邊形
，那么是否存在點，使四邊形為菱形？若存在，請求出此時點的坐標(biāo)；若不存在，請說明理由；
（3）如圖2，過拋物線頂點
作直線
軸，交
軸于點
，點
是拋物線上、兩點間的一個動點（點不與、兩點重合），直線
、
與直線
分別交于點
、
，當(dāng)點運動時，
是否為定值？若是，試求出該定值；若不是，請說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知
的半徑為 4，
是圓的直徑，點
是的切線
上的一個動點，連接
交于點
，弦
平行于，連接
.
(1)試判斷直線
與的位置關(guān)系，并說明理由；
(2)當(dāng)
__________時，四邊形
為菱形；
(3)當(dāng)
___________時，四邊形
為正方形.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
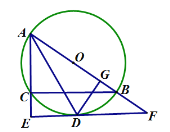
【題目】如圖，⊙O是△ABC的外接圓，AB為⊙O的直徑，過點A作AD平分∠BAC交⊙O于點D，過點D作BC的平行線分別交AC、AB的延長線于點E、F，DG⊥AB于點G，連接BD．
(1)求證：△AED∽△DGB；
(2)求證：EF是⊙O的切線；
(3)若
，OA＝4，求劣弧
的長度(結(jié)果保留π)．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com