【題目】如圖，已知雙曲線y=
（k＜0）經過直角三角形OAB斜邊OA的中點D，且與直角邊AB相交于點C．若點A的坐標為（﹣8，4），則△AOC的面積為（ ）
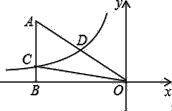
A. 6 B. 12 C. 18 D. 24
【答案】B
【解析】
已知A點坐標
，且D點為直角三角形OAB斜邊的中點，由三角形的性質可知點D的坐標，將D點坐標代入反比例函數
可以解得k的值，又直角邊AB和反比例函數相交于點C，結合圖像和反比例函數可知C點坐標，從而可以求出△OBC的面積，用大三角形OAB減去小三角形OBC的面積求出△AOC的面積.
∵點D是Rt△OAB斜邊的中點，且點A坐標，∴點D坐標
，將點D坐標代入反比例函數
中有
，∴反比例函數
∵線段AB與反比例函數交于點C結合圖像知C點橫坐標為－8，代入反比例函數，∴
，∴D點坐標為
，∵△OAB為直角三角形，∴∠ABO＝90°，所以S△OAB＝
×8×4＝16,S△OBC＝×8×1＝4,∴S△AOC＝S△OAB－S△OBC＝16－4＝12，故本題答案選擇B.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
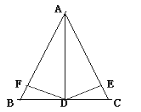
【題目】如圖：在△ABC中，AD是∠BAC的平分線，DE⊥AC于E，DF⊥AB于F，且FB=CE，則下列結論：①DE=DF，②AE=AF，③BD=CD，④AD⊥BC。
其中正確的有___________ (填序號)。
查看答案和解析>>
科目：初中數學 來源： 題型：
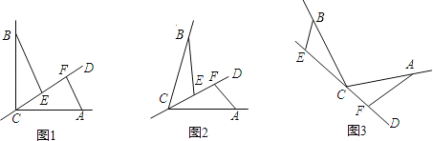
【題目】CD經過∠BCA頂點C的一條直線，CA=CB．E，F分別是直線CD上兩點，且∠BEC=∠CFA=∠α．
（1）若直線CD經過∠BCA的內部，且E，F在射線CD上，請解決下面兩個問題：
①如圖1，若∠BCA=90°，∠α=90°，則BE_____CF；EF_____|BE﹣AF|（填“＞”，“＜”或“=”）；
②如圖2，若0°＜∠BCA＜180°，請添加一個關于∠α與∠BCA關系的條件_____，使①中的兩個結論仍然成立。
（2）如圖3，若直線CD經過∠BCA的外部，∠α=∠BCA，請提出EF，BE，AF三條線段數量關系的合理猜想并給出理由。．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知A（2 
，2）、B（2 ，1），將△AOB繞著點O逆時針旋轉，使點A旋轉到點A′（﹣2 
，2 ）的位置，則圖中陰影部分的面積為 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
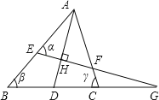
【題目】如圖，AD平分∠BAC，EG⊥AD于H，則下列等式中成立的是 ( )
A. ∠α=
（∠β﹣∠γ） B. ∠α=（∠β+∠γ） C. ∠G=（∠β+∠γ） D. ∠G=∠α
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
