
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 在拋物線
在拋物線![]() (
(![]() )上,且
)上,且![]() ,
,
(1)若![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)若該拋物線與![]() 軸交于點
軸交于點![]() ,其對稱軸與
,其對稱軸與![]() 軸交于點
軸交于點![]() ,試求出
,試求出![]() ,
,![]() 的數(shù)量關系;
的數(shù)量關系;
(3)將該拋物線平移,平移后的拋物線仍經(jīng)過![]() ,點
,點![]() 的對應點
的對應點![]() ,當
,當![]() 時,求平移后拋物線的頂點所能達到的最高點的坐標.
時,求平移后拋物線的頂點所能達到的最高點的坐標.
【答案】(1)b=1,c=3;(2)![]() ;(3)(
;(3)(![]() ,
,![]() )
)
【解析】
(1)把![]() 代入
代入![]() 得
得![]() ,與
,與![]() 構成方程組,解方程組即可求得;
構成方程組,解方程組即可求得;
(2)求得![]() ,
,![]() ,
,![]() ,即可得到
,即可得到![]() ,
,![]() ,即可求得
,即可求得![]() ;
;
(3)把![]() 化成頂點式,得到
化成頂點式,得到![]() ,根據(jù)平移的規(guī)律得到
,根據(jù)平移的規(guī)律得到![]() ,把
,把![]() 代入,進一步得到
代入,進一步得到![]() ,即
,即![]() ,分類求得
,分類求得![]() ,由
,由![]() ,得到
,得到![]() ,即
,即![]() ,從而得到平移后的解析式為
,從而得到平移后的解析式為![]() ,得到頂點為
,得到頂點為![]() ,
,![]() ,設
,設![]() ,即
,即![]() ,即可得到
,即可得到![]() 取最大值為
取最大值為![]() ,從而得到最高點的坐標.
,從而得到最高點的坐標.
解:(1)把![]() 代入
代入![]() ,可得
,可得![]() ,
,
解![]() ,可得
,可得![]() ,
,![]() ;
;
(2)由![]() ,得
,得![]() .
.
對于![]() ,
,
當![]() 時,
時,![]() .
.
拋物線的對稱軸為直線![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
因為![]() ,
,
所以![]() ,
,![]() ,
,
![]() ;
;
(3)由平移前的拋物線![]() ,可得
,可得
![]() ,即
,即![]() .
.
因為平移后![]() 的對應點為
的對應點為![]()
可知,拋物線向左平移![]() 個單位長度,向上平移
個單位長度,向上平移![]() 個單位長度.
個單位長度.
則平移后的拋物線解析式為![]() ,
,
即![]() .
.
把![]() 代入,得
代入,得![]() .
.
![]() .
.
![]() ,
,
所以![]() .
.
當![]() 時,
時,![]() (不合題意,舍去);
(不合題意,舍去);
當![]() 時,
時,![]() ,
,
因為![]() ,所以
,所以![]() .
.
所以![]() ,
,
所以平移后的拋物線解析式為![]() .
.
即頂點為![]() ,
,![]() ,
,
設![]() ,即
,即![]() .
.
因為![]() ,所以當
,所以當![]() 時,
時,![]() 隨
隨![]() 的增大而增大.
的增大而增大.
因為![]() ,
,
所以當![]() 時,
時,![]() 取最大值為
取最大值為![]() ,
,
此時,平移后拋物線的頂點所能達到的最高點坐標為![]() ,
,![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】在國家政策的調控下,某市的商品房成交均價由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7兩月平均每月降價的百分率;
(2)如果房價繼續(xù)回落,按此降價的百分率,請你預測到9月份該市的商品房成交均價是否會跌破每平方米6500元?請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
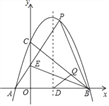
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)與x軸交于點A(﹣1,0),B(4,0),與y軸交于點C(0,4).
(1)求此拋物線的解析式;
(2)設點P(2,n)在此拋物線上,AP交y軸于點E,連接BE,BP,請判斷△BEP的形狀,并說明理由;
(3)設拋物線的對稱軸交x軸于點D,在線段BC上是否存在點Q,使得△DBQ成為等腰直角三角形?若存在,求出點Q的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】松雷中學校學生會干部對校學生會倡導的“助殘”自愿捐款活動進行抽樣調查,得到一組學生捐款情況的數(shù)據(jù),下圖是根據(jù)這組數(shù)據(jù)繪制的統(tǒng)計圖,圖中從左到右各長方形高度之比為3:4:5:8:2,又知此次調查中捐15元和20元的人數(shù)共39人.
(1)他們一共抽查了多少人?
(2)若該校共有2310名學生,請估計全校學生共捐款多少元?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,以△ABC的邊BC為直徑的⊙O交AC于點D,過點D作⊙O的切線交AB于點E.
(1)如圖1,若∠ABC=90°,求證:OE∥AC;
(2)如圖2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
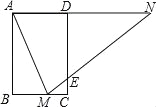
【題目】如圖,矩形ABCD中,AB=3,BC=2,點M在BC上,連接AM,作∠AMN=∠AMB,點N在直線AD上,MN交CD于點E
(1)求證:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)當M為BC中點時,求ME的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
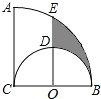
【題目】如圖,![]() ,
,![]() ,以BC為直徑作半圓,圓心為點O;以點C為圓心,BC為半徑作
,以BC為直徑作半圓,圓心為點O;以點C為圓心,BC為半徑作![]() ,過點O作AC的平行線交兩弧于點D、E,則陰影部分的面積是
,過點O作AC的平行線交兩弧于點D、E,則陰影部分的面積是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com