
【題目】在平面直角坐標系中,函數圖象![]() 上點
上點![]() 的橫坐標
的橫坐標![]() 與其縱坐標
與其縱坐標![]() 的和
的和![]() 稱為點
稱為點![]() 的“坐標和”,而圖象
的“坐標和”,而圖象![]() 上所有點的“坐標和”中的最小值稱為圖象
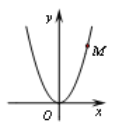
上所有點的“坐標和”中的最小值稱為圖象![]() 的“智慧數”.如圖:拋物線
的“智慧數”.如圖:拋物線![]() 上有一點
上有一點![]() ,則點
,則點![]() 的“坐標和”為6,當
的“坐標和”為6,當![]() 時,該拋物線的“智慧數”為0.
時,該拋物線的“智慧數”為0.
(1)點![]() 在函數
在函數![]() 的圖象上,點
的圖象上,點![]() 的“坐標和”是 ;
的“坐標和”是 ;
(2)求直線![]() 的“智慧數”;
的“智慧數”;
(3)若拋物線![]() 的頂點橫、縱坐標的和是2,求該拋物線的“智慧數”;
的頂點橫、縱坐標的和是2,求該拋物線的“智慧數”;
(4)設拋物線![]() 頂點的橫坐標為
頂點的橫坐標為![]() ,且該拋物線的頂點在一次函數
,且該拋物線的頂點在一次函數![]() 的圖象上;當
的圖象上;當![]() 時,拋物線
時,拋物線![]() 的“智慧數”是2,求該拋物線的解析式.
的“智慧數”是2,求該拋物線的解析式.
【答案】(1)4;(2)直線![]() “智慧數”等于
“智慧數”等于![]() ;(3)拋物線
;(3)拋物線![]() 的“智慧數”是
的“智慧數”是![]() ;(4)拋物線的解析式為
;(4)拋物線的解析式為![]() 或
或![]()
【解析】
(1)先求出點N的坐標,然后根據“坐標和”的定義計算即可;
(2)求出![]() ,然后根據一次函數的增減性和“智慧數”的定義計算即可;
,然后根據一次函數的增減性和“智慧數”的定義計算即可;
(3)先求出拋物線的頂點坐標,即可列出關于b和c的等式,然后求出![]() ,然后利用二次函數求出y+x的最小值即可得出結論;
,然后利用二次函數求出y+x的最小值即可得出結論;
(4)根據題意可設二次函數為![]() ,坐標和為
,坐標和為![]() ,即可求出
,即可求出![]() 與x的二次函數關系式,求出
與x的二次函數關系式,求出![]() 與x的二次函數圖象的對稱軸,先根據已知條件求出m的取值范圍,然后根據
與x的二次函數圖象的對稱軸,先根據已知條件求出m的取值范圍,然后根據![]() 與對稱軸的相對位置分類討論,分別求出
與對稱軸的相對位置分類討論,分別求出![]() 的最小值列出方程即可求出結論.
的最小值列出方程即可求出結論.
解:(1)將y=2代入到![]() 解得x=2
解得x=2
∴點N的坐標為(2,2)
∴點![]() 的“坐標和”是2+2=4
的“坐標和”是2+2=4
故答案為:4;
(2)![]() ,
,
∵![]() ,
,
∴當![]() 時,
時,![]() 最小,
最小,
即直線![]() ,“智慧數”等于
,“智慧數”等于![]()
(3)拋物線的頂點坐標為![]() ,
,
∴![]() ,即
,即![]()
![]()
∵![]() ,
,
∴![]() 的最小值是
的最小值是![]()
∴拋物線![]() 的“智慧數”是
的“智慧數”是![]() ;
;
(4)∵二次函數![]() 的圖象的頂點在直線
的圖象的頂點在直線![]() 上,
上,
∴設二次函數為![]() ,坐標和為
,坐標和為![]()
![]()
對稱軸![]()
∵![]()
∴![]()
①當![]() 時,即
時,即![]() 時,“坐標和”隨
時,“坐標和”隨![]() 的增大而增大
的增大而增大
∴把![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
當![]() 時,
時,![]()
②當![]() ,即
,即![]() 時,
時,
![]() ,即
,即![]() ,
,
解得![]() ,
,
當![]() 時,
時,![]()
③當![]() 時,
時,![]()
∵![]() ,所以此情況不存在
,所以此情況不存在
綜上,拋物線的解析式為![]() 或
或![]()


科目:初中數學 來源: 題型:
【題目】某同學報名參加校運動會,有以下5個項目可供選擇:徑賽項目:100m,200m,![]() 分別用
分別用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田賽項目:跳遠,跳高
;田賽項目:跳遠,跳高![]() 分別用
分別用![]() 、
、![]() 表示
表示![]() .
.
![]() 該同學從5個項目中任選一個,恰好是田賽項目的概率為______;
該同學從5個項目中任選一個,恰好是田賽項目的概率為______;
![]() 該同學從5個項目中任選兩個,利用樹狀圖或表格列舉出所有可能出現的結果,并求恰好是一個田賽項目和一個徑賽項目的概率.
該同學從5個項目中任選兩個,利用樹狀圖或表格列舉出所有可能出現的結果,并求恰好是一個田賽項目和一個徑賽項目的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小華設計的“作一個角等于已知角的2倍”的尺規作圖過程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
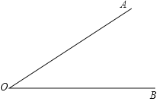
作法:如圖,
①在射線![]() 上任取一點
上任取一點![]() ;
;
②作線段![]() 的垂直平分線,交
的垂直平分線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ;
;
③連接![]() ;
;
所以![]() 即為所求作的角.
即為所求作的角.
根據小華設計的尺規作圖過程,
(1)使用直尺和圓規補全圖形(保留作圖痕跡);
(2)完成下面的證明(說明:括號里填寫推理的依據).
證明:∵![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形網格中,![]() .線段
.線段![]() 與線段
與線段![]() 存在一種變換關系,即其中一條線段繞著某點旋轉一個角度可以得到另一條線段,則這個旋轉中心的坐標為__________.
存在一種變換關系,即其中一條線段繞著某點旋轉一個角度可以得到另一條線段,則這個旋轉中心的坐標為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
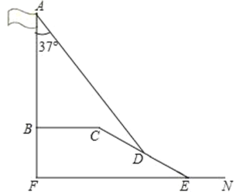
【題目】在學習解直角三角形以后,重慶八中數學興趣小組測量了旗桿的高度,如圖,某一時刻,旗桿AB的影子一部分落在平臺上,另一部分落在斜坡上,測得落在平臺上的影長BC為6米,落在斜坡上的影長CD為4米,AB⊥BC,同一時刻,光線與旗桿的夾角為37°,斜坡CE的坡角為30°,旗桿的高度約為多少米?(結果精確到0.1,參考數據:sin37°=0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】去年某市為創評“全國文明城市”稱號,周末團市委組織志愿者進行宣傳活動.班主任梁老師決定從 4 名女班干部(小悅、小文、小雅和小宇)中通過抽簽方式確定 2 名女生去參加.抽簽規則:將 4 名女班干部姓名分別寫在 4 張完全相同的卡片正面,把四張卡片背面朝上,洗勻后放在桌面上,梁老師先從中隨機抽取一張卡片,記下姓名,再從剩余的 3張卡片中隨機抽取第二張,記下姓名.
(1)該班男生“小安被抽中”是 事件,“小悅被抽中”是 事件(填“不可能”或“必然”或“隨機”);第一次抽取卡片“小文被抽中”的概率為 ;
(2)試用畫樹狀圖或列表的方法表示這次抽簽所有可能的結果,并求出“小雅被抽中”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
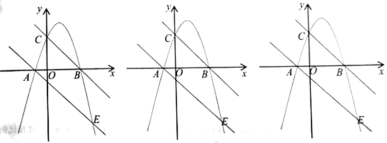
【題目】如圖,拋物線![]() 經過
經過![]() ,
,![]() 兩點,且與
兩點,且與![]() 軸交于點
軸交于點![]() ,拋物線與直線
,拋物線與直線![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)求拋物線的解析式;
(2)坐標軸上是否存在一點![]() ,使得
,使得![]() 是以
是以![]() 為底邊的等腰三角形?若存在,請直接寫出點
為底邊的等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
(3)![]() 點在
點在![]() 軸上且位于點
軸上且位于點![]() 的左側,若以
的左側,若以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
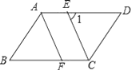
【題目】如圖,在ABCD中,CE平分∠BCD,且交AD于點E,AF∥CE,且交BC于點F.
(1)求證:△ABF≌△CDE;
(2)如圖,若∠B=52°,求∠1的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com