
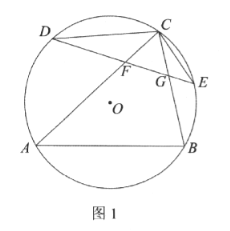
【題目】如圖1,![]() 內接于
內接于![]() 分別是
分別是![]() 和
和![]() 所對弧的中點,弦
所對弧的中點,弦![]() 分別交
分別交![]() 于點
于點![]() ,連結
,連結![]()
(1)求證:![]() 是等邊三角形.
是等邊三角形.
(2)若![]()
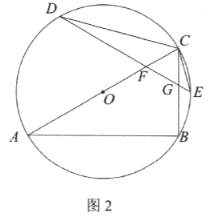
①如圖2,當![]() 為
為![]() 的直徑時,求
的直徑時,求![]() 的長.
的長.
②當![]() 將
將![]() 的面積分成了
的面積分成了![]() 的兩部分時,求
的兩部分時,求![]() 的長.
的長.
(3)連結![]() 交
交![]() 于點
于點![]() ,若
,若![]() :則
:則![]() 的值為_______. (請直接寫出答案)
的值為_______. (請直接寫出答案)
【答案】(1)見解析;(2)①8;②![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)利用弧的關系證得![]() ,
,![]() ,利用三角形外角的性質證得∠CFG=60°,從而證得
,利用三角形外角的性質證得∠CFG=60°,從而證得![]() 是等邊三角形;
是等邊三角形;
(2)①連結OD,利用![]() 求得直徑AC的長,得到半徑OD=
求得直徑AC的長,得到半徑OD=![]() ,證得∠DOC=90°,在Rt
,證得∠DOC=90°,在Rt![]() 中,再利用
中,再利用![]() 即可求解;
即可求解;
②利用弧的關系![]() =120°=
=120°=![]() ,證得DE=AB=12,分DF:FG=2:1或DF:FG=1:2兩種情況討論,證得△DCF△CEG,利用對應邊成比例分別計算即可求解;
,證得DE=AB=12,分DF:FG=2:1或DF:FG=1:2兩種情況討論,證得△DCF△CEG,利用對應邊成比例分別計算即可求解;
(3)作出如圖的輔助線,設![]() ,
,![]() ,得到
,得到![]() ,證得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分別求得BC、EF、EG、DF、FA的長,即可求解.
,證得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分別求得BC、EF、EG、DF、FA的長,即可求解.
(1)∵∠ACB=60°,
∴優弧![]() =120°,
=120°,
∴![]() ,
,
∵D,E分別是![]() ,
,![]() 的中點,
的中點,
∴![]() ,
,
∴∠ACD+∠EDC=60°=∠CFG,
∵∠ACB=60°,
∴△CFG是等邊三角形;
(2)①連結OD,
∵AC是圓O的直徑,AB=12,
∴∠B=90°,
∵∠ACB=60°,
![]() ,
,
∴AC=![]() ,
,
∴OD=![]() ,
,
由(1)得:△CFG為等邊三角形,
∴∠CFG=60![]() ,
,
∵點D是![]() 的中點,
的中點,
∴∠DOC=90°,
∵∠DFO=∠CFG=60°,
![]() ,
,
∴DF=8;
②由(1)得:![]() ,
,
∵D、E分別是![]() 、
、![]() 的中點,
的中點,
∴![]() =120°=
=120°=![]() ,
,
∴DE=AB=12,
ⅰ)當DF:FG=2:1時,
設FG=![]() ,DF=2
,DF=2![]() ,
,
由(1)得:△CFG為等邊三角形,
∴![]() ,GE=12-3
,GE=12-3![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,![]() ,
,
∴∠DCA=∠CED,∠CDE=∠ECB,
∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,
,
連結OD交AC于點M,
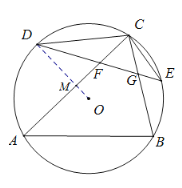
∵D是![]() 的中點,
的中點,
∴OD⊥AC,
在Rt△DMF中,∠DFM=∠CFG=60°,
∴FM=![]() DF=
DF=![]() ,
,
∴AC=2(FM+CF)= 2(![]() +
+![]() )=
)= ![]() ;
;
ⅱ)當DF:FG=1:2時,
設DF=![]() ,FG=CF=CG=2
,FG=CF=CG=2![]() ,GE=12-3
,GE=12-3![]() ,
,
同理,∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
即DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,CF=
,CF=![]() ,
,
同理得AC=![]() ;
;
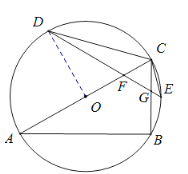
(3)作CP∥FD交BD延長線于點P,連接AD,
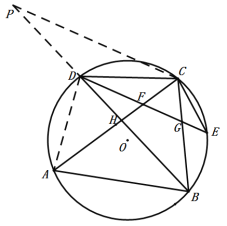
∵點D、E分別是![]() 、
、![]() 的中點,
的中點,
∴∠CDF=∠FDH,AD=DC,
∵CP∥FD,
∴∠FDC=∠DCP,∠CPD=∠FDH,![]() ,
,
∴∠DCP=∠CPD,
∴PD=CD,
∴![]() ,
,
∵![]() ,
,
∴設![]() ,
,![]() ,則
,則![]() ,
,
∴![]() ,
,
∵![]() ,∠AHD=∠BHC,
,∠AHD=∠BHC,
∴∠DAH=∠CBH,
∴△AHD∽△BHC,
∴![]() ,即
,即![]() ,
,
∴ ,
,
∴![]() ;
;
由(1)得:△CFG為等邊三角形,
∴![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,
∴∠HBC=∠CEF,
∴△HBC∽△CEF,
∴![]() ,即
,即 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠DBG=∠CEG,∠DGB=∠CGE,
∴△DBG∽△CEG,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
同理:∴△DFA∽△CFE,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
∴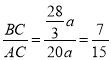 .
.
故答案為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 過A(-1,0)、B(3,0),直線AD交拋物線于點D,點D的橫坐標為2,點P(m,n)是線段AD上的動點.
過A(-1,0)、B(3,0),直線AD交拋物線于點D,點D的橫坐標為2,點P(m,n)是線段AD上的動點.
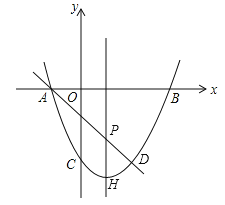
(1)求拋物線和直線AD的解析式;
(2)過點P的直線垂直于x軸,交拋物線于點H,
①求線段PH的長度l與m的關系式;
②當PH=2時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)與x軸交于點A、B,與y軸分別交于點C,其中點A(﹣1,0),OB=4OA,OC=2OA
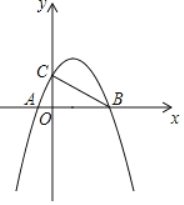
(1)求拋物線的解析式.
(2)點P是線段AB一動點,過P作PD∥AC交BC于D,當△PCD面積最大時,求點P的坐標.
(3)點M是位于線段BC上方的拋物線上一點,當∠ABC恰好等于△BCM中的某個角時,直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
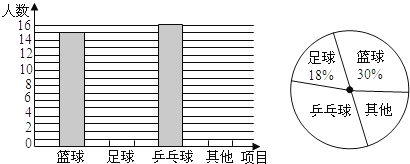
【題目】在大課間活動中,同學們積極參加體育鍛煉,小明就本班同學“我最喜愛的體育項目”進行了一次調查統計,下面是他通過收集數據后,繪制的兩幅不完整的統計圖.請你根據圖中提供的信息,解答以下問題:
(1)該班共有 名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,“乒乓球”部分所對應的圓心角度數為 ;
(4)學校將舉辦體育節,該班將推選5位同學參加乒乓球活動,有3位男同學(A,B,C)和2位女同學(D,E),現準備從中選取兩名同學組成雙打組合,用樹狀圖或列表法求恰好選出一男一女組成混合雙打組合的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年突如其來的肺炎疫情,給我們的生活和學習帶來了諸多不便.圖1是2月1日至2月5日全國“新冠肺炎”疫情新增數據統計圖,為了控制疫情蔓延擴散,國家全面落實疫情防控工作,舉國上下眾志成城,圖2是3月5日至3月9日全國“新冠肺炎”疫情新增數據統計圖,請根據統計圖解答以下問題:
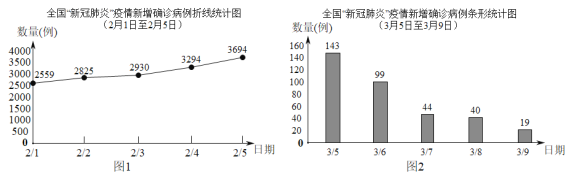
(1)寫出2月3日全國新增確診病例數,并計算3月5日至3月9日全國新增確診病例數的平均數.
(2)對比兩幅統計圖中的數據,選擇一個角度分析評價此次疫情控制情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
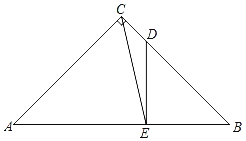
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=BC=4,點D在邊BC上,且BD=3CD,DE⊥AB,垂足為點E,聯結CE.
(1)求線段AE的長;
(2)求∠ACE的余切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小微企業為加快產業轉型升級步伐,引進一批A,B兩種型號的機器.已知一臺A型機器比一臺B型機器每小時多加工2個零件,且一臺A型機器加工80個零件與一臺B型機器加工60個零件所用時間相等.
(1)每臺A,B兩種型號的機器每小時分別加工多少個零件?
(2)如果該企業計劃安排A,B兩種型號的機器共10臺一起加工一批該零件,為了如期完成任務,要求兩種機器每小時加工的零件不少于72件,同時為了保障機器的正常運轉,兩種機器每小時加工的零件不能超過76件,那么A,B兩種型號的機器可以各安排多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com