
【題目】定義:兩條長度相等,且它們所在的直線互相垂直的線段,我們稱其互為“等垂線段”.
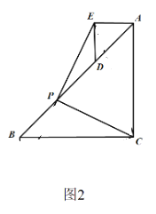
知識應用:在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC, ∠ACB=∠AED=90°,連接BD,點P是線段BD的中點,連接PC,PE.
(1)如圖1,當AE在線段AC上時,線段PC與線段PE是否互為“等垂線段”?請說明理由.
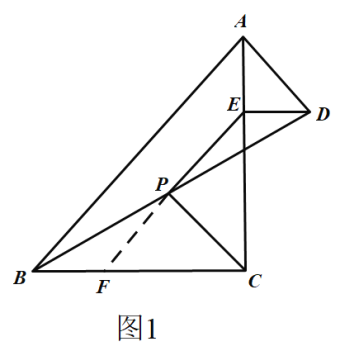
(2)如圖2,將圖1中的△ADE繞點A順時針旋轉90°,點D落在AB邊上,請說明線段PC與線段PE互為“等垂線段”.
拓展延伸:(3)將圖1中的△ADE繞點A順時針旋轉150°,若BC=3,DE=1,求PC的值.

【答案】(1)線段PC與線段PE互為“等垂線段”,理由見解析;(2)見解析;(3)![]()
【解析】
(1)延長EP交BC于點F,首先證明![]() ,則有PF=PE=
,則有PF=PE=![]() EF,BF=DE,然后證明△EFC是等腰直角三角形,再利用等腰直角三角形的性質即可證明線段PC與線段PE互為“等垂線段”;
EF,BF=DE,然后證明△EFC是等腰直角三角形,再利用等腰直角三角形的性質即可證明線段PC與線段PE互為“等垂線段”;
(2)作BF//DE,交EP的延長線于點F,連接CE,CF,首先證明![]() ,則有BF= DE, PE=PF=
,則有BF= DE, PE=PF=![]() EF,然后利用平行線的性質得出∠CBF=∠CAE,進而可證
EF,然后利用平行線的性質得出∠CBF=∠CAE,進而可證![]() ,則有CF=CE,∠FCB=∠ECA,從而得出△FCE是等腰直角三角形,則結論可證;
,則有CF=CE,∠FCB=∠ECA,從而得出△FCE是等腰直角三角形,則結論可證;
(3)作BF//DE,交EP的延長線于點F,連接CE,CF,過點E作EH⊥AC交CA的延長線于點H,首先證明![]() ,則有BF= DE, PE=PF=
,則有BF= DE, PE=PF=![]() EF,然后可證
EF,然后可證![]() ,則有CF=CE,∠FCB=∠ECA,從而得出△FCE是等腰直角三角形,則PC=PE=
,則有CF=CE,∠FCB=∠ECA,從而得出△FCE是等腰直角三角形,則PC=PE=![]() EC,然后在Rt
EC,然后在Rt![]() AHE中,求出HE,AH的長度,進而求出CH的長度,然后在Rt
AHE中,求出HE,AH的長度,進而求出CH的長度,然后在Rt![]() CEH中,由勾股定理求出EC的長度,則PC的長度可求 .
CEH中,由勾股定理求出EC的長度,則PC的長度可求 .
解:(1)線段PC與線段PE互為“等垂線段”.
理由:如圖1,延長EP交BC于點F.
∵∠ACB=∠AED=90°,
∴DE![]() BC,
BC,
∴∠EDP=∠FBP.
∵點P是線段BD的中點,
∴PB=PD.
在![]() 和
和![]() 中,
中,
![]()
∴PF=PE=![]() EF,BF=DE.
EF,BF=DE.
∵AC=BC,AE=DE,
∴AC﹣AE=BC﹣BF,即EC=FC.
又∵∠ACB=90°,
∴△EFC是等腰直角三角形.
∵EP=FP,
∴PC=PE,PC⊥PE,
∴線段PC與線段PE互為“等垂線段”;
(2)如圖2,作BF//DE,交EP的延長線于點F,連接CE,CF,
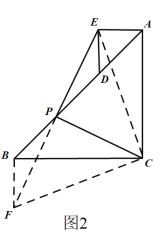
∵DE![]() BF,
BF,
∴∠EDP=∠FBP.
∵點P是線段BD的中點,
∴PB=PD.
在![]() 和
和![]() 中,
中,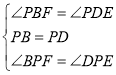
![]()
∴BF= DE, PE=PF=![]() EF.
EF.
∵DE=AE,
∴BF=AE.
∵∠CAE=90°,∠AED=90°,
∴ED![]() AC.
AC.
![]() ,
,
∴FB![]() AC,
AC,
∴![]() ,
,
∴∠CBF=∠CAE.
在![]() 和
和![]() 中,
中,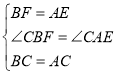
![]()
∴CF=CE,∠FCB=∠ECA.
∵∠ACB=90°,
∴∠FCE=90°,
∴△FCE是等腰直角三角形.
∵PE=PF,
∴PC⊥PE,PC=PE,
∴線段PC與線段PE互為“等垂線段”;
(3)如圖3
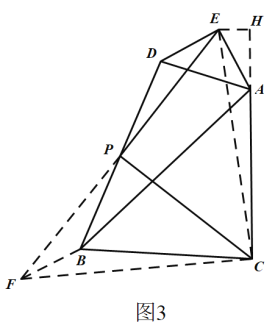
作BF//DE,交EP的延長線于點F,連接CE,CF,過點E作EH⊥AC交
當旋轉角為150°時,由旋轉可知,∠CAE=150°,DE與BC所夾的銳角為30°,
∴∠FBC=∠EAC=150°.
∵DE![]() BF,
BF,
∴∠EDP=∠FBP.
∵點P是線段BD的中點,
∴PB=PD.
在![]() 和
和![]() 中,
中,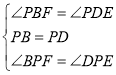
![]()
∴BF= DE, PE=PF=![]() EF.
EF.
∵DE=AE ,
∴BF=AE.
在![]() 和
和![]() 中,
中,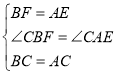
![]()
∴CF=CE,∠FCB=∠ECA.
∵∠ACB=90° ,
∴∠FCE=90°,
∴△FCE是等腰直角三角形.
∵PE=PF,
∴PC⊥PE,PC=PE=![]() EC.
EC.
在Rt![]() AHE中,∠EAH=30°,AE=DE=1,
AHE中,∠EAH=30°,AE=DE=1,
∴HE=![]() ,AH=
,AH=![]() .
.
又∵AC=BC=3,
∴CH=AC+AH=3+![]() .
.
在Rt![]() CEH中,
CEH中,
由勾股定理得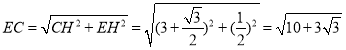 ,
,
![]() .
.


科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() . 點
. 點![]() 是平面內不與點
是平面內不與點![]() 重合的任意一點, 連接
重合的任意一點, 連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]()
(1)動手操作
如圖1,當![]() 時,我們通過用 刻度尺和量角器度量發現:
時,我們通過用 刻度尺和量角器度量發現:
![]() 的值是
的值是![]() ;直線
;直線![]() 與直線
與直線![]() 相交所成的較小角的度數是
相交所成的較小角的度數是![]() ;
;
請證明以上結論正確.
(2)類比探究
如圖2,當![]() 時,請寫出
時,請寫出![]() 的值及直線
的值及直線![]() 與直線
與直線![]() 相交所成的較小角的度數,并就圖2的情形說明理由.
相交所成的較小角的度數,并就圖2的情形說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,把矩形沿AC折疊,點B落在點E處,AE與DC的交點為O,連接DE.
(1)求證:△ADE≌△CED;
(2)求證:DE∥AC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了迎接體育中考,某校九(1)班的體育老師對全班45名學生進行了一次體育模擬測試(得分均為整數),成績滿分為10分,該班的體育委員根據這次測試成績,制作了統計圖和分析表如下:
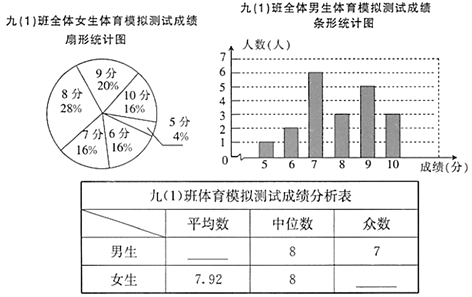
根據以上信息,解答下列問題.
(1)這個班共有男生_________人,女生有____________人.
(2)請你補全九(1)班體育模擬測試成績分析表.
(3)你認為在這次體育模擬測試中,九(1)班的全體男生和全體女生,誰的表現更好一些?請寫出一條支持你的看法的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市對即將參加中考的4000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖.請根據圖表信息回答下列問題:
初中畢業生視力抽樣調查頻數分布表
視力 | 頻數(人) | 頻率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次調查樣本容量為 ;
(2)在頻數分布表中,a= ,b= ,并將頻數分布直方圖補充完整;
(3)若視力在4.9以上(含4.9)均屬標準視力,根據上述信息估計全區初中畢業生中達到標準視力的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為激發學生的閱讀興趣,培養學生良好的閱讀習慣,我區某校欲購進一批學生喜歡的圖書,學校組織學生會隨機抽取部分學生進行問卷調查,被調查學生須從“文史類、社科類、小說類、生活類”中選擇自己喜歡的一類,根據調查結果繪制了統計圖(未完成),請根據圖中信息,解答下列問題:
(1)填空或選擇:此次共調查了______名學生;圖2中“小說類”所在扇形的圓心角為______度;學生會采用的調查方式是______.A.普查 B.抽樣調查
(2)將條形統計圖(圖1)補充完整;
(3)若該校共有學生2500人,試估計該校喜歡“社科類”書籍的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系 xOy 中,將點 A(2,4)向下平移 2 個單位得到點 C,反比例函數y ![]() (m≠0)的圖象經過點 C,過點 C 作 CB⊥x 軸于點 B
(m≠0)的圖象經過點 C,過點 C 作 CB⊥x 軸于點 B

(1)求 m 的值;
(2)一次函數 y=kx+b(k<0)的圖象經過點 C,交 x 軸于點 D, 線段 CD,BD,BC 圍成的區域(不含邊界)為 G; 若橫、縱坐標都是整數的點叫做整點
①b=3 時,直接寫出區域 G 內的整點個數
②若區域 G 內沒有整點,結合函數圖象,確定 k 的取值范圍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,對折矩形紙片ABCD,使AD與BC重合,得到折痕EF,把紙片展平,再一次折疊紙片,使點A落在EF上的點A′處,并使折痕經過點B,得到折痕BM,若矩形紙片的寬AB=4,則折痕BM的長為( )
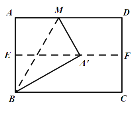
A.![]() B.
B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com