
如圖,已知:△ABC中,∠C=Rt∠,AC=BC,P是AB上任一點.
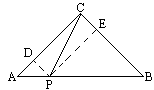
求證:AP2+BP2=2PC2.
|
證法一:過P點作PD⊥AC,PE⊥BC,垂足分別為D、E,容易證明 AD=PD,BE=PE=CE. 在Rt△APD中,AP2=AD2+PD2=2PD2. 在Rt△BPE中, BP2=BE2+PE2=2PE2=2CD2. ∴AP2+BP2=2PD2+2CD2=2(PD2+CD2). 在Rt△PCD中,PC2=PD2+CD2.∴AP2+BP2=2PC2. 證法二:如圖,過C點作CD⊥AB,垂足為D.
∵AC=BC,∠ACB=Rt∠, ∴AD=BD=CD. ∴AP2+BP2=(AD-PD)2+(BD+PD)2 =(CD-PD)2+(CD+PD)2 =CD2-2CD·PD+PD2+CD2+2CD·PD+PD2 =2(CD2+PD2). 在Rt△PDC中,PC2=CD2+PD2,AP2+BP2=2PC2. |
|
注:在構(gòu)造直角二角形證線段的平方和或平方差時,可以發(fā)現(xiàn)往往一題有多種處理手段,同學(xué)們在平時處理問題的過程中,應(yīng)加以分析理解,從而達到消化吸收的目的.值得提出的是:方法二中的變換是代數(shù)的恒等變形,在幾何證明中經(jīng)常用到,應(yīng)引起同學(xué)們的注意和重視. |


 導(dǎo)學(xué)與測試系列答案
導(dǎo)學(xué)與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數(shù)學(xué) 來源: 題型:
| 1 | 3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
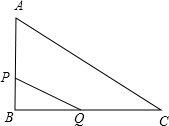
 如圖,已知:△ABC為等邊三角形,D、F分別為射線BC、射線AB邊上的點,BD=AF,以AD為邊作等邊△ADE.
如圖,已知:△ABC為等邊三角形,D、F分別為射線BC、射線AB邊上的點,BD=AF,以AD為邊作等邊△ADE.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
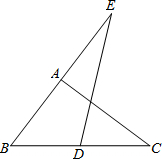 如圖,已知在△ABC中,D是邊BC的中點,點E在邊BA的延長線上,AE=AB,
如圖,已知在△ABC中,D是邊BC的中點,點E在邊BA的延長線上,AE=AB,| BA |
| a |
| BC |
| b |
| DE |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com