
【題目】如圖,在等邊三角形![]() 中,在
中,在![]() 邊上取兩點(diǎn)
邊上取兩點(diǎn)![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 則以
, 則以![]() ,
,![]() ,
,![]() 為邊長的三角形的形狀為( )
為邊長的三角形的形狀為( )

A.銳角三角形B.直角三角形C.鈍角三角形D.隨![]() ,
,![]() ,
,![]() 的值而定
的值而定
【答案】C
【解析】
將△ABM繞點(diǎn)B順時(shí)針旋轉(zhuǎn)60![]() 得到△CBH.連接HN.想辦法證明∠HCN=120
得到△CBH.連接HN.想辦法證明∠HCN=120![]() ,HN=MN=x即可解決問題;
,HN=MN=x即可解決問題;
將△ABM繞點(diǎn)B順時(shí)針旋轉(zhuǎn)60![]() 得到△CBH.連接HN.
得到△CBH.連接HN.
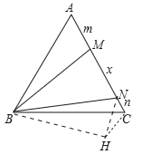
∵△ABC是等邊三角形,
∴∠ABC=∠ACB=∠A=60![]() ,
,
∵∠MON=30![]() ,
,
∴∠ABM+∠CBN=30![]() ,
,
∴∠NBH=∠CBH+∠CBN=30![]() ,
,
∴∠NBM=∠NBH,
∵BM=BH,BN=BN,
∴△NBM≌△NBH,
∴MN=NH=x,
∵∠BCH=∠A=60![]() ,CH=AM=n,
,CH=AM=n,
∴∠NCH=120![]() ,
,
∴x,m,n為邊長的三角形△NCH是鈍角三角形,
故選:C.


 應(yīng)用題天天練四川大學(xué)出版社系列答案
應(yīng)用題天天練四川大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() 、
、![]() 是對(duì)角線
是對(duì)角線![]() 上的兩點(diǎn)且
上的兩點(diǎn)且![]() ,下列說法中正確的是( )
,下列說法中正確的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④四邊形
;④四邊形![]() 為平行四邊形;⑤
為平行四邊形;⑤![]() ;⑥
;⑥![]() .
.

A.①⑥B.①②④⑥C.①②③④D.①②④⑤⑥
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù) ![]() 的圖象經(jīng)過A(2,0),B(0,-6)兩點(diǎn).
的圖象經(jīng)過A(2,0),B(0,-6)兩點(diǎn).
(1)求這個(gè)二次函數(shù)的解析式及頂點(diǎn)坐標(biāo);
(2)設(shè)該二次函數(shù)的對(duì)稱軸與x軸交于點(diǎn)C,連接BA,BC,求△ABC的面積.
(3)在拋物線的對(duì)稱軸上是否存在一點(diǎn)P.使得以O(shè)、B、C、P四點(diǎn)為頂點(diǎn)的四邊形是平行四邊形?若存在,請(qǐng)直接寫出P點(diǎn)坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校組織了全校1500名學(xué)生參加傳統(tǒng)文化知識(shí)網(wǎng)絡(luò)競賽.賽后隨機(jī)抽取了其中200名學(xué)生的成績作為樣本進(jìn)行整理,并制作了如下不完整的頻數(shù)分布表和頻數(shù)分布直方圖.
成績(分) | 頻數(shù)(人) | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
請(qǐng)根據(jù)圖表提供的信息,解答下列各題:
(1)表中m= ,n= ,請(qǐng)補(bǔ)全頻數(shù)分布直方圖;
(2)若用扇形統(tǒng)計(jì)圖來描述成績分布情況,則分?jǐn)?shù)段80≤x<90對(duì)應(yīng)扇形的圓心角的度數(shù)是 ;
(3)若成績?cè)?/span>80分以上(包括80分)為合格,則參加這次競賽的1500名學(xué)生中成績合格的大約有多少名?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】教材在探索平方差公式時(shí)利用了面積法,面積法除了可以幫助我們記憶公式,還可以直觀地推導(dǎo)或驗(yàn)證公式,俗稱“無字證明”,例如,著名的趙爽弦圖(如圖①,其中四個(gè)直角三角形較大的直角邊長都為![]() ,較小的直角邊長都為
,較小的直角邊長都為![]() ,斜邊長都為
,斜邊長都為![]() ),大正方形的面積可以表示為
),大正方形的面積可以表示為![]() ,也可以表示為
,也可以表示為![]() ,由此推導(dǎo)出重要的勾股定理:如果直角三角形兩條直角邊長為
,由此推導(dǎo)出重要的勾股定理:如果直角三角形兩條直角邊長為![]() ,斜邊長為
,斜邊長為![]() ,則
,則![]() .
.
(1)圖②為美國第二十任總統(tǒng)伽菲爾德的“總統(tǒng)證法”,請(qǐng)你利用圖②推導(dǎo)勾股定理.
(2)如圖③,在![]() 中,
中,![]() 是
是![]() 邊上的高,
邊上的高,![]() ,
,![]() ,
,![]() ,設(shè)
,設(shè)![]() ,求
,求![]() 的值.
的值.
(3)試構(gòu)造一個(gè)圖形,使它的面積能夠解釋![]() ,畫在如圖4的網(wǎng)格中,并標(biāo)出字母
,畫在如圖4的網(wǎng)格中,并標(biāo)出字母![]() 所表示的線段.
所表示的線段.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,點(diǎn)D是BC邊上的一點(diǎn),∠B=50°,∠BAD=30°,將△ABD沿AD折疊得到△AED,AE與BC交于點(diǎn)F.
(1)填空:∠ADC= 度;
(2)當(dāng)∠C=20°時(shí),判斷DE與AC的位置關(guān)系,并說明理由。

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
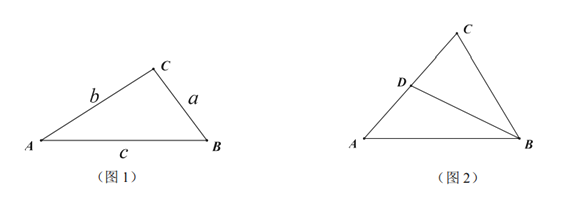
【題目】如圖1,![]() 的
的![]() 所對(duì)邊分別是
所對(duì)邊分別是![]() ,且
,且![]() ,若滿足
,若滿足![]() ,則稱
,則稱![]() 為奇異三角形,例如等邊三角形就是奇異三角形.
為奇異三角形,例如等邊三角形就是奇異三角形.
(1)若![]() ,判斷
,判斷![]() 是否為奇異三角形,并說明理由;
是否為奇異三角形,并說明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(3)如圖2,在奇異三角形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上的中點(diǎn),連結(jié)
邊上的中點(diǎn),連結(jié)![]() ,
,![]() 將
將![]() 分割成2個(gè)三角形,其中
分割成2個(gè)三角形,其中![]() 是奇異三角形,
是奇異三角形,![]() 是以
是以![]() 為底的等腰三角形,求
為底的等腰三角形,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將平行四邊形紙片![]() 沿對(duì)角線
沿對(duì)角線![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 落在平行四邊形
落在平行四邊形![]() 所在平面內(nèi),
所在平面內(nèi),![]() 和
和![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,連接
,連接![]()
![]() 判斷
判斷![]() 和
和![]() 的位置關(guān)系,并證明.
的位置關(guān)系,并證明.
![]() 在圖1中,若
在圖1中,若![]() ,是否存在
,是否存在![]() 恰好為直角三角形的情形?若存在,求出
恰好為直角三角形的情形?若存在,求出![]() 的長度:若不存在,請(qǐng)說明理由.
的長度:若不存在,請(qǐng)說明理由.
![]() 若將圖中平行四邊形紙片
若將圖中平行四邊形紙片![]() 換成矩形紙片
換成矩形紙片![]() ,沿對(duì)角線折疊發(fā)現(xiàn)所得圖形是軸對(duì)稱圖形;將所得圖形沿其對(duì)稱軸再次折疊后,得到的仍是軸對(duì)稱圖形.則矩形紙片
,沿對(duì)角線折疊發(fā)現(xiàn)所得圖形是軸對(duì)稱圖形;將所得圖形沿其對(duì)稱軸再次折疊后,得到的仍是軸對(duì)稱圖形.則矩形紙片![]() 的長寬之比是多少?請(qǐng)直接寫出結(jié)果.
的長寬之比是多少?請(qǐng)直接寫出結(jié)果.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com