
【題目】如圖①,在平面直角坐標系中,拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,將直線
,將直線![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() 的度數后與該拋物線交于
的度數后與該拋物線交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),點
的左側),點![]() 是該拋物線上一點
是該拋物線上一點
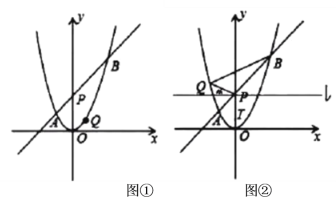
(1)若![]() ,求直線
,求直線![]() 的函數表達式
的函數表達式
(2)若點![]() 將線段分成
將線段分成![]() 的兩部分,求點
的兩部分,求點![]() 的坐標
的坐標
(3)如圖②,在(1)的條件下,若點![]() 在
在![]() 軸左側,過點
軸左側,過點![]() 作直線
作直線![]() 軸,點
軸,點![]() 是直線
是直線![]() 上一點,且位于
上一點,且位于![]() 軸左側,當以
軸左側,當以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似時,求
相似時,求![]() 的坐標
的坐標
【答案】(1)![]() ;(2)
;(2)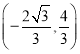 或
或![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根據題意易得點M、P的坐標,利用待定系數法來求直線AB的解析式;
(2)分![]() 和
和![]() 兩種情況根據點A、點B在直線y=x+2上列式求解即可;
兩種情況根據點A、點B在直線y=x+2上列式求解即可;
(3)分![]() 和
和![]() 兩種情況,利用相似三角形的性質列式求解即可.
兩種情況,利用相似三角形的性質列式求解即可.
(1)如圖①,設直線AB與x軸的交點為M.
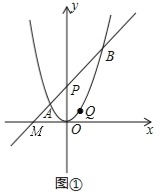
∵∠OPA=45°,
∴OM=OP=2,即M(-2,0).
設直線AB的解析式為y=kx+b(k≠0),將M(-2,0),P(0,2)兩點坐標代入,得
![]() ,
,
解得,![]() .
.
故直線AB的解析式為y=x+2;
(2)①![]()
設![]()
![]() (a>0)
(a>0)
∵點A、點B在直線y=x+2上和拋物線y=x2的圖象上,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
解得,![]() ,
,![]() (舍去)
(舍去)
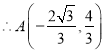
②![]()
設![]()
![]() (a>0)
(a>0)
∵點A、點B在直線y=x+2上和拋物線y=x2的圖象上,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
解得:![]() ,
,![]() (舍去)
(舍去)
![]()
綜上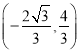 或
或![]()
(3)![]() ,
,![]()
![]() ,
,![]()
①![]()
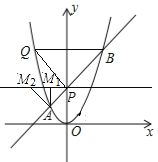
此時![]() ,
,![]() 關于
關于![]() 軸對稱,
軸對稱,![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]()
②![]()
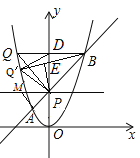
此時![]() 滿足,左側還有
滿足,左側還有![]() 也滿足
也滿足
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 四點共圓,易得圓心為
四點共圓,易得圓心為![]() 中點
中點![]()
設![]() ,
,![]()
∵![]()
![]()
![]()
![]() 且不與
且不與![]() 重合
重合
![]()
![]() ,
,![]()
![]()
![]() 為正三角形,
為正三角形,
![]()
過![]() 作
作![]() ,則
,則![]() ,
,![]()
![]()
∵![]()
∴![]()
∴![]()
解得,![]()
∴![]()
∵![]()
∴![]()
∴![]()
解得,![]()
∴![]()
綜上所述,滿足條件的點M的坐標為:![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
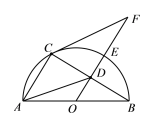
【題目】如圖,AB是半圓O的直徑,D為弦BC的中點,延長OD交弧BC于點E,點F為OD的延長線上一點且滿足∠OBC=∠OFC,
(1)求證:CF為⊙O的切線;
(2)若四邊形ACFD是平行四邊形,求sin∠BAD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的頂點坐標分別為A(-2,4),B(4,4),C(6,0).
(1)△ABC的面積是 .
(2)請以原點O為位似中心,畫出△A'B'C',使它與△ABC的相似比為1:2,變換后點A、B的對應點分別為點A'、B',點B'在第一象限;
(3)若P(a,b)為線段BC上的任一點,則變換后點P的對應點P' 的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,是一建筑物造型的縱截面,曲線![]() 是拋物線的一部分,該拋物線開口向右、對稱軸正好是水平線
是拋物線的一部分,該拋物線開口向右、對稱軸正好是水平線![]() ,
,![]() ,
,![]() 是與水平線
是與水平線![]() 垂直的兩根支柱,
垂直的兩根支柱,![]() 米,
米,![]() 米,
米,![]() 米.
米.
(1)如圖1,為了安全美觀,準備拆除支柱![]() 、
、![]() ,在水平線
,在水平線![]() 上另找一點
上另找一點![]() 作為地面上的支撐點,用固定材料連接
作為地面上的支撐點,用固定材料連接![]() 、
、![]() ,對拋物線造型進行支撐加固,用料最省時點
,對拋物線造型進行支撐加固,用料最省時點![]() ,
,![]() 之間的距離是_________.
之間的距離是_________.
(2)如圖2,在水平線![]() 上增添一張
上增添一張![]() 米長的椅子
米長的椅子![]() (
(![]() 在
在![]() 右側),用固定材料連接
右側),用固定材料連接![]() 、
、![]() ,對拋物線造型進行支撐加固,用料最省時點
,對拋物線造型進行支撐加固,用料最省時點![]() ,
,![]() 之間的距離是_______________.
之間的距離是_______________.
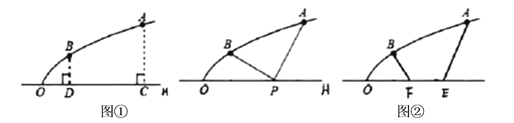
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O為∠ABC的邊![]() 上的一點,過點O作OM⊥AB于點
上的一點,過點O作OM⊥AB于點![]() ,到點
,到點![]() 的距離等于線段OM的長的所有點組成圖形
的距離等于線段OM的長的所有點組成圖形![]() .圖形W與射線
.圖形W與射線![]() 交于E,F兩點(點在點F的左側).
交于E,F兩點(點在點F的左側).
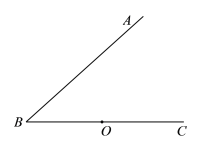
(1)過點![]() 作
作![]() 于點
于點![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的長;
,求MH的長;
(2)將射線BC繞點B順時針旋轉得到射線BD,使得∠![]()
![]() ,判斷射線BD與圖形
,判斷射線BD與圖形![]() 公共點的個數,并證明.
公共點的個數,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() 的圖像與x軸相交于點A,與y軸相交于點B,二次函數
的圖像與x軸相交于點A,與y軸相交于點B,二次函數![]() 圖像經過點A、B,與x軸相交于另一點C.
圖像經過點A、B,與x軸相交于另一點C.
(1)求a、b的值;
(2)在直角坐標系中畫出該二次函數的圖像;
(3)求∠ABC的度數.
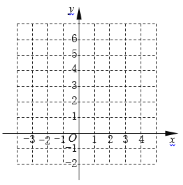
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作半圓⊙O,交BC于點D,連接AD.過點D作DE⊥AC,垂足為點E.
(1)求證:DE是⊙O的切線;
(2)當⊙O半徑為3,CE=2時,求BD長.
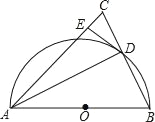
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,以AC為直徑的⊙O交AB于點D,點E為弧AD的中點,連接CE交AB于點F,且BF=BC.

(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為2,![]() =
=![]() ,求CE的長.
,求CE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com