
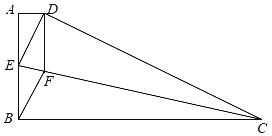
【題目】如圖,四邊形ABCD中,AD//BC,∠A=90°,CD=CB,過點C作∠DCB的平分線CE交AB于點E,連接DE,過點D作DF//AB,且交CE于F點,連接BF.
(1)求證:四邊形DEBF是菱形;
(2)若AB=5,BC=13,求tan∠AED的值.
【答案】(1)見解析;(2)tan∠AED=![]() .
.
【解析】
(1)證明△CDE≌△CBE,根據全等三角形的性質得到ED=EB,∠DEC=∠BEC,根據平行線的性質、等腰三角形的判定定理得到DE=DF,根據菱形的判定定理證明;
(2)根據矩形的性質得到∠BGD=90°,DG=AB=5,AD=BG,根據勾股定理求出GC,求出AD,根據勾股定理列方程求出AE,根據正切的定義計算,得到答案.
解:(1)證明:∵CE平分∠DCB,
∴∠DCE=∠BCE,
在△CDE和△CBE中,
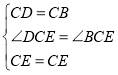
∴△CDE≌△CBE(SAS),
∴ED=EB,∠DEC=∠BEC,
∵DF//AB,
∴∠DFE=∠BEC,
∴∠DFE=∠DEC,
∴DE=DF,
∴DF=BE,又DF//AB,DE=DF,
∴四邊形DEBF為菱形;
(2)∵AD//BC,AB//DF,
∴四邊形ABGD為平行四邊形,
∵∠A=90°,
∴四邊形ABGD為矩形,
∴∠BGD=90°,DG=AB=5,AD=BG,
在Rt△DGC中,GC=![]() =12,
=12,
∴AD=BG=BC﹣GC=13﹣12=1,
設AE=x,則DE=BE=5﹣x,
在Rt△ADE中,DE2=AE2+AD2,即(5﹣x)2=x2+12,
解得,x=![]() ,
,
∴tan∠AED=![]() =
=![]() .
.


科目:初中數學 來源: 題型:
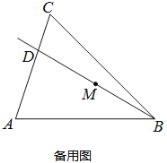
【題目】如圖,在△ABC中,![]() ,tanA=3,∠ABC=45°,射線BD從與射線BA重合的位置開始,繞點B按順時針方向旋轉,與射線BC重合時就停止旋轉,射線BD與線段AC相交于點D,點M是線段BD的中點.
,tanA=3,∠ABC=45°,射線BD從與射線BA重合的位置開始,繞點B按順時針方向旋轉,與射線BC重合時就停止旋轉,射線BD與線段AC相交于點D,點M是線段BD的中點.
(1)求線段BC的長;
(2)①當點D與點A、點C不重合時,過點D作DE⊥AB于點E,DF⊥BC于點F,連接ME,MF,在射線BD旋轉的過程中,∠EMF的大小是否發生變化?若不變,求∠EMF的度數;若變化,請說明理由.
②在①的條件下,連接EF,直接寫出△EFM面積的最小值______.

查看答案和解析>>
科目:初中數學 來源: 題型:
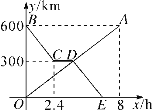
【題目】貨車和轎車分別從甲、乙兩地同時出發,沿同一公路相向而行.轎車出發2.4h后休息,直至與貨車相遇后,以原速度繼續行駛.設貨車出發xh后,貨車、轎車分別到達離甲地y1km和y2km的地方,圖中的線段OA、折線BCDE分別表示y1、y2與x之間的函數關系.
(1)求點D的坐標,并解釋點D的實際意義;
(2)求線段DE所在直線的函數表達式;
(3)當貨車出發________h時,兩車相距200km.
查看答案和解析>>
科目:初中數學 來源: 題型:
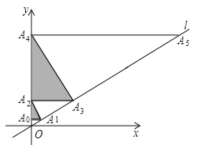
【題目】如圖,過點![]() 作
作![]() 軸的垂線交直線
軸的垂線交直線![]() 于點
于點![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,交
的垂線,交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線交直線
軸的垂線交直線![]() 于點
于點![]() …,這樣依次下去,得到
…,這樣依次下去,得到![]() ,…,其面積分別記為
,…,其面積分別記為![]() ,…,則
,…,則![]() 為__________.
為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 分別是
分別是![]() 的中點,連接
的中點,連接![]() .
.
(1)探索發現:

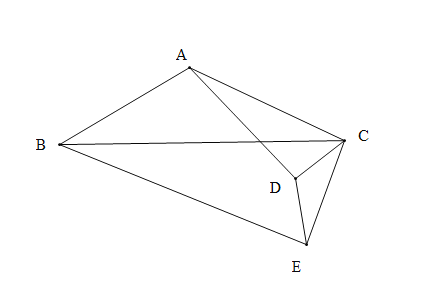
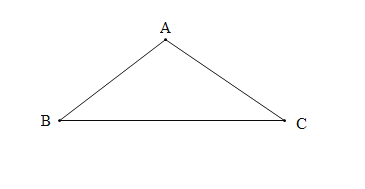
圖1中,![]() 的值為_____________;
的值為_____________;![]() 的值為_________.
的值為_________.
(2)拓展探究
若將![]() 繞點
繞點![]() 逆時針方向旋轉一周,在旋轉過程中
逆時針方向旋轉一周,在旋轉過程中![]() 的大小有無變化?請僅就圖2的情形給出證明.
的大小有無變化?請僅就圖2的情形給出證明.
(3)問題解決
當![]() 旋轉至
旋轉至![]() 三點在同一直線時,直接寫出線段
三點在同一直線時,直接寫出線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
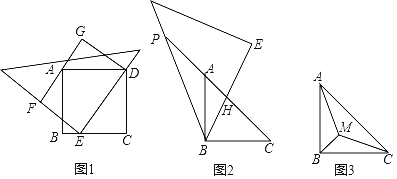
【題目】已知,把45°的直三角板的直角頂點E放在邊長為6的正方形ABCD的一邊BC上,直三角板的一條直角邊經過點D,以DE為一邊作矩形DEFG,且GF過點A,得到圖1.
(1)求矩形DEFG的面積;
(2)若把正方形ABCD沿著對角線AC剪掉一半得到等腰直角三角形ABC,把45°的直三角板的一個45°角的頂點與等腰直角三角形ABC的直角頂點B重合,直三角板夾這個45°角的兩邊分別交CA和CA的延長線于點H、P,得到圖2.猜想:CH、PA、HP之間的數量關系,并說明理由;
(3)若把邊長為6的正方形ABCD沿著對角線AC剪掉一半得到等腰直角三角形ABC,點M是Rt△ABC內一個動點,連接MA、MB、MC,設MA+MB+MC=y,直接寫出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在5×5的正方形網格,每個小正方形的邊長都為1,線段AB的端點落在格點上,要求畫一個四邊形,所作的四邊形為中心對稱圖形,同時滿足下列要求:
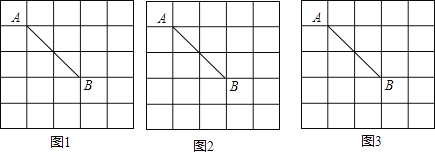
(1)在圖1中畫出以AB為一邊的四邊形;
(2)分別在圖2和圖3中各畫出一個以AB為一條對角線的四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
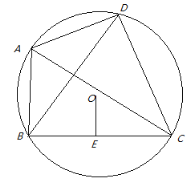
【題目】如圖,已知:四邊形ABCD內接于⊙O,對角線AC⊥BD,⊙O的半徑為6cm,AD=4cm,OE⊥BC,垂足為E.則弦BC的長為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
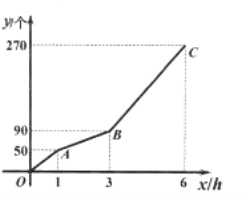
【題目】甲、乙兩臺機器共同加工一批零件,一共用了![]() 小時.在加工過程中乙機器因故障停止工作,排除故障后,乙機器提高了工作效率且保持不變,繼續加工.甲機器在加工過程中工作效率保持不變.甲、乙兩臺機器加工零件的總數
小時.在加工過程中乙機器因故障停止工作,排除故障后,乙機器提高了工作效率且保持不變,繼續加工.甲機器在加工過程中工作效率保持不變.甲、乙兩臺機器加工零件的總數![]() (個)與甲加工時間
(個)與甲加工時間![]() 之間的函數圖象為折線
之間的函數圖象為折線![]() ,如圖所示.
,如圖所示.
(1)這批零件一共有 個,甲機器每小時加工 個零件,乙機器排除故障后每小時加工 個零件;
(2)當![]() 時,求
時,求![]() 與
與![]() 之間的函數解析式;
之間的函數解析式;
(3)在整個加工過程中,甲加工多長時間時,甲與乙加工的零件個數相等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com