
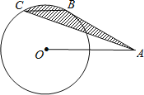
【題目】如圖,A是半徑為2的⊙O外的一點,OA=4,AB切⊙O于點B,弦BC∥OA,連接AC,則圖中陰影部分的面積為___________
【答案】![]() π
π
【解析】
連接OB、OC,如圖,利用切線的性質得∠ABO=90°,再利用直角三角形的性質可求出∠BAO=30°,則∠AOB=60°,接著利用平行線的性質得到∠CBO=∠AOB=60°,利用三角形面積公式可得到S△ABC=S△OCB,然后根據扇形的面積公式,利用圖中陰影部分的面積=S扇形BOC進行計算.
解:連接OB、OC,如圖,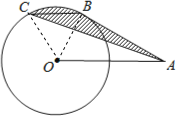
∵AB切⊙O于點B,
∴OB⊥AB,
∴∠ABO=90°,
在Rt△ABO中,∵OA=4,OB=2,
∴∠BAO=30°,
∴∠AOB=60°,
∵BC∥OA,
∴∠CBO=∠AOB=60°,S△ABC=S△OCB,
∴∠BOC=60°,圖中陰影部分的面積=S扇形BOC,
∴圖中陰影部分的面積=![]() =
=![]() π.
π.
故答案為![]() π.
π.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD的四個角向內折疊鋪平,恰好拼成一個無縫隙無重疊的矩形EFGH,若EH=5,EF=12,則矩形ABCD的面積是( )
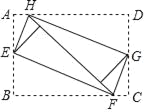
A. 13 B. ![]() C. 60 D. 120
C. 60 D. 120
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社區決定把一塊長![]() ,寬
,寬![]() 的矩形空地建成居民健身廣場,設計方案如圖,陰影區域為綠化區(四塊綠化區為大小、形狀都相同的矩形),空白區域為活動區,且四周的4個出口寬度相同,其寬度不小于
的矩形空地建成居民健身廣場,設計方案如圖,陰影區域為綠化區(四塊綠化區為大小、形狀都相同的矩形),空白區域為活動區,且四周的4個出口寬度相同,其寬度不小于![]() ,不大于
,不大于![]() ,設綠化區較長邊為
,設綠化區較長邊為![]() ,活動區的面積為
,活動區的面積為![]() .為了想知道出口寬度的取值范圍,小明同學根據出口寬度不小于
.為了想知道出口寬度的取值范圍,小明同學根據出口寬度不小于![]() ,算出
,算出![]() .
.
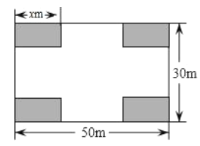
(1)求![]() 與
與![]() 的函數關系式并直接寫出自變量
的函數關系式并直接寫出自變量![]() 的取值范圍;
的取值范圍;
(2)求活動區的最大面積;
(3)預計活動區造價為50元/![]() ,綠化區造價為40元/
,綠化區造價為40元/![]() ,若社區的此項建造投資費用不得超過72000元,求投資費用最少時活動區的出口寬度?
,若社區的此項建造投資費用不得超過72000元,求投資費用最少時活動區的出口寬度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖線段AB的端點在邊長為1的正方形網格的格點上,現將線段AB繞點A按逆時針方向旋轉90°得到線段AC.

(1)請你用尺規在所給的網格中畫出線段AC及點B經過的路徑;
(2)若將此網格放在一平面直角坐標系中,已知點A的坐標為(1,3),點B的坐標為(-2,-1),則點C的坐標為 ;
(3)線段AB在旋轉到線段AC的過程中,線段AB掃過的區域的面積為 ;
(4)若有一張與(3)中所說的區域形狀相同的紙片,將它圍成一個幾何體的側面,則該幾何體底面圓的半徑長為
查看答案和解析>>
科目:初中數學 來源: 題型:
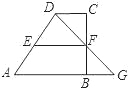
【題目】如圖,梯形ABCD中,AB∥CD,點F在BC上,連DF與AB的延長線交于點G.
(1)求證:△CDF∽△BGF;
(2)當點F是BC的中點時,過F作EF∥CD交AD于點E,若AB=6cm,EF=4cm,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
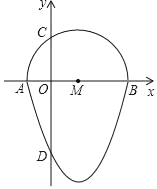
【題目】如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”.已知點A、B、C、D分別是“果圓”與坐標軸的交點,拋物線的解析式為y=x2﹣6x﹣16,AB為半圓的直徑,則這個“果圓”被y軸截得的線段CD的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
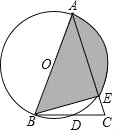
【題目】如圖,在△ABC中,AB=AC,E在AC上,經過A,B,E三點的圓O交BC于點D,且D點是弧BE的中點,
(1)求證AB是圓的直徑;
(2)若AB=8,∠C=60°,求陰影部分的面積;
(3)當∠A為銳角時,試說明∠A與∠CBE的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,二次函數![]() 的圖象經過A(3,3),與x軸正半軸交于B點,與y軸交于C點,△ABC的外接圓恰好經過原點O.
的圖象經過A(3,3),與x軸正半軸交于B點,與y軸交于C點,△ABC的外接圓恰好經過原點O.
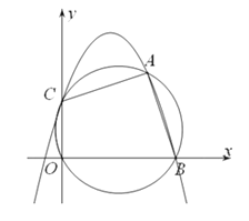
(1)求B點的坐標及二次函數的解析式;
(2)拋物線上一點Q(m,m+3),(m為整數),點M為△ABC的外接圓上一動點,求線段QM長度的范圍;
(3)將△AOC繞平面內一點P旋轉180°至△A'O'C'(點O'與O為對應點),使得該三角形的對應點中的兩個點落在![]() 的圖象上,求出旋轉中心P的坐標.
的圖象上,求出旋轉中心P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com