
【題目】如圖,在菱形ABCD中,∠B=60°,BC=6,E為BC中點,F是AB上一點,G為AD上一點,且BF=2,∠FEG=60°,EG交AC于點H,下列結論:①△BEF∽△CHE;②AG=1;③EH=![]() ;④S△BEF=3S△AGH;正確的是______.(填序號即可)
;④S△BEF=3S△AGH;正確的是______.(填序號即可)
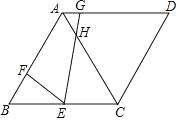
【答案】①②③
【解析】
①菱形的性質以及一線三等角即可證明△BEF∽△CHE,故①正確;
②由△BEF∽△CHE,可得![]() ,從而求得CH,由此可得AH,由△AGH∽△CEH,可得
,從而求得CH,由此可得AH,由△AGH∽△CEH,可得![]() ,從而求得AH=1,故②正確;
,從而求得AH=1,故②正確;
③過H作HM⊥BC于點M,在Rt△HMC中,HM=HC·sin60![]() ,MC=HC·sin30=
,MC=HC·sin30=![]() ,可得ME=EC-MC=
,可得ME=EC-MC=![]() ,在Rt△MEH中,由勾股定理可得EH=
,在Rt△MEH中,由勾股定理可得EH=![]() ,故③正確;
,故③正確;
④由△BEF∽△CHE,△AHG∽△CHE,可得△BEF∽△AHG,即![]() ,即S△BEF=4S△AGH,故④錯誤,故答案為:①②③
,即S△BEF=4S△AGH,故④錯誤,故答案為:①②③
①∵四邊形ABCD是菱形,∠B=60 ,BC=6,
∴AB=BC=AC=6,
∵∠CEH+∠FEH+∠FEB=180 ,∠B+∠FEB+∠BFE=180 ,∠B=∠FEH =60 ,
∴∠BFE=∠CEH,
∴△BEF∽△CHE,故①正確;
②∵E是BC的中點,
∴BE=CE=3,
∵△BEF∽△CHE,
∴![]() ,即
,即![]() ,
,
∴CH=![]() ,
,
∴AH=AC-CH=6-![]() =
=![]() ,
,
∵AD∥BC,
∴△AGH∽△CEH,
∴![]() ,即
,即![]() ,
,
∴AH=1,故②正確;
③過H作HM⊥BC于點M,
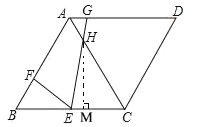
在Rt△HMC中,∠C=60,HC=![]() ,
,
∴HM=HC·sin60=![]() ,
,
MC=HC·sin30=![]() ,
,
∴ME=EC-MC=3-![]() =
=![]() ,
,
在Rt△MEH中,HE=![]() =
=![]() ,故③正確;
,故③正確;
④∵△BEF∽△CHE,△AHG∽△CHE,
∴△BEF∽△AHG,
∴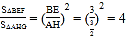 ,
,
即S△BEF=4S△AGH,故④錯誤,
故答案為:①②③


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】一個不透明的袋子中裝有三個完全相同的小球,分別標有數字3、4、5.從袋子中隨機取出一個小球,用小球上的數字作為十位的數字,然后放回;再取出一個小球,用小球上的數字作為個位上的數字,這樣組成一個兩位數,試問:按這種方法能組成哪些位數?十位上的數字與個位上的數字之和為9的兩位數的概率是多少?用列表法或畫樹狀圖法加以說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
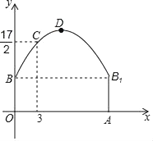
【題目】如圖,隧道的截面由拋物線和長方形構成,長方形的長是12m,寬是4m.按照圖中所示的直角坐標系,拋物線最高點D到墻面OB的水平距離為6m時,隧道最高點D距離地面10m.
(1)求該拋物線的函數關系式;
(2)一輛貨運汽車載一長方體集裝箱后寬為4m,高為6m,如果隧道內設雙向行車道,那么這輛貨車能否安全通過?
(3)在拋物線型拱壁上需要安裝兩排燈,使它們離地面的高度相等,如果燈離地面的高度不超過8m,那么兩排燈的水平距離最小是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:甲、乙兩車分別從相距200千米的![]() ,
,![]() 兩地同時出發相向而行,其中甲車到
兩地同時出發相向而行,其中甲車到![]() 地后立即返回,下圖是它們離各自出發地的距離
地后立即返回,下圖是它們離各自出發地的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)之間的函數圖象.
(小時)之間的函數圖象.
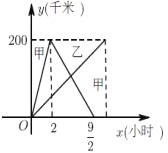
(1)求甲車離出發地的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)之間的函數關系式,并寫出自變量的取值范圍.
(小時)之間的函數關系式,并寫出自變量的取值范圍.
(2)當![]() 時,甲、乙兩車離各自出發地的距離相等,求乙車離出發地的距離
時,甲、乙兩車離各自出發地的距離相等,求乙車離出發地的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)之間的函數關系式,并寫出自變量的取值范圍.
(小時)之間的函數關系式,并寫出自變量的取值范圍.
(3)在(2)的條件下,求它們在行駛的過程中相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=90°,AB=AC=1,點D是BC上一個動點(不與B、C重合),在AC上取E點,使∠ADE=45度.
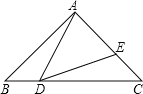
(1)求證:△ABD∽△DCE;
(2)設BD=x,AE=y,求y關于x的函數關系式;
(3)當:△ADE是等腰三角形時,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
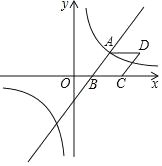
【題目】如圖,已知一次函數y=![]() x﹣3與反比例函數y=
x﹣3與反比例函數y=![]() 的圖象相交于點A(4,n),與x軸相交于點B.
的圖象相交于點A(4,n),與x軸相交于點B.
(1)填空:n的值為____,k的值為______;
(2)以AB為邊作菱形ABCD,使點C在x軸正半軸上,點D在第一象限,求點D的坐標;
(3)觀察反比例函數y=![]() 的圖象,當y≥﹣3時,請直接寫出自變量x的取值范圍.
的圖象,當y≥﹣3時,請直接寫出自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘海上巡邏船在A地巡航,這時接到B地海上指揮中心緊急通知:在指揮中心北偏西60°方向的C地有一艘漁船遇險,要求馬上前去救援,要求馬上前去救援.此時C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B兩地之間的距離為12海里,則A、C兩地之間的距離為________.
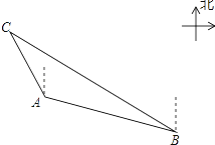
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為美化校園,準備在長35米,寬20米的長方形場地上,修建若干條寬度相同的道路,余下部分作草坪,并請全校學生參與方案設計,現有3位同學各設計了一種方案,圖紙分別如圖l、圖2和圖3所示(陰影部分為草坪).

請你根據這一問題,在每種方案中都只列出方程不解.
①甲方案設計圖紙為圖l,設計草坪的總面積為600平方米.
②乙方案設計圖紙為圖2,設計草坪的總面積為600平方米.
③丙方案設計圖紙為圖3,設計草坪的總面積為540平方米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一張矩形紙片,長10cm,寬6cm,在它的四角各減去一個同樣的小正方形,然后折疊成一個無蓋的長方體紙盒.若紙盒的底面(圖中陰影部分)面積是32cm2,求剪去的小正方形的邊長.設剪去的小正方形邊長是xcm,根據題意可列方程為( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com