
【題目】觀察下列等式,探究發(fā)現(xiàn)規(guī)律,并解決問(wèn)題,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接寫(xiě)出第④個(gè)等式: ;
(2)猜想第![]() 個(gè)等式(用含字母
個(gè)等式(用含字母![]() 的式子表示),并說(shuō)明這個(gè)等式的正確性;
的式子表示),并說(shuō)明這個(gè)等式的正確性;
(3)利用發(fā)現(xiàn)的規(guī)律,求![]() 的值.(參考數(shù)據(jù):
的值.(參考數(shù)據(jù):![]() )
)
【答案】(1)35﹣34=2×34;(2)猜想:第n個(gè)等式為:3n+1﹣3n=2×3n.理由見(jiàn)解析;(3)88572
【解析】
(1)根據(jù)已知規(guī)律寫(xiě)出④即可.
(2)根據(jù)已知規(guī)律寫(xiě)出n個(gè)等式,利用提公因式法即可證明規(guī)律的正確性.
(3)根據(jù)發(fā)現(xiàn)的規(guī)律得到(32-31)+(33-32)+(34-33)+…+(311-310)=2(31+32+33+…+310),依此可求31+32+33+…+310的值.
(1)①![]() ;
;
②![]() ;
;
③![]() ;
;
∴第④個(gè)等式:35-34=2×34;
故答案為:35-34=2×34;
(2)猜想:第n個(gè)等式為:3n+1﹣3n=2×3n.
理由如下:
∵3n+1﹣3n=3×3n﹣3n=(3﹣1)×3n=2×3n,
∴3n+1﹣3n=2×3n;
(3)根據(jù)發(fā)現(xiàn)的規(guī)律,有:311﹣310=2×310,
∴(32﹣31)+(33﹣32)+(34﹣33)+…+(311﹣310)=2(31+32+33+…+310),
∴311﹣31=2(31+32+33+…+310),
即31+32+33+…+310=![]() (311﹣3).
(311﹣3).
∵311=177147,
∴31+32+33+…+310=![]() (177147﹣3)=88572.
(177147﹣3)=88572.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知等腰三角形ABC的底角為30°,以BC為直徑的⊙O與底邊AB交于點(diǎn)D,過(guò)D作DE⊥AC,垂足為E.
(1)證明:DE為⊙O的切線;
(2)連接OE,若BC=4,求△OEC的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象交于A(m,6),B(3,n)兩點(diǎn).
的圖象交于A(m,6),B(3,n)兩點(diǎn).
(1)求一次函數(shù)的解析式;
(2)求![]() 的面積;
的面積;
(3)根據(jù)圖象直接寫(xiě)出![]() 的x的取值范圍
的x的取值范圍

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線與![]() 軸交于
軸交于![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() ,
,![]() 為拋物線上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)
為拋物線上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,拋物線的對(duì)稱(chēng)軸是直線
,拋物線的對(duì)稱(chēng)軸是直線![]() .
.
(1)求拋物線的函數(shù)表達(dá)式和直線![]() 的解析式;
的解析式;
(2)若點(diǎn)![]() 在第二象限內(nèi),且
在第二象限內(nèi),且![]() ,求
,求![]() 的面積;
的面積;
(3)在(2)的條件下,若![]() 為直線
為直線![]() 上一點(diǎn),是否存在點(diǎn)
上一點(diǎn),是否存在點(diǎn)![]() ,使
,使![]() 為等腰三角形?若存在,直接寫(xiě)出點(diǎn)
為等腰三角形?若存在,直接寫(xiě)出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
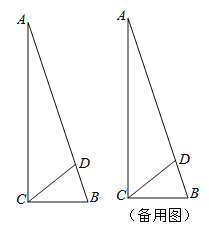
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是斜邊上一點(diǎn),且
是斜邊上一點(diǎn),且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)過(guò)點(diǎn)![]() 的
的![]() 與邊
與邊![]() 相切,切點(diǎn)為
相切,切點(diǎn)為![]() 的中點(diǎn)
的中點(diǎn)![]() ,
,![]() 與直線
與直線![]() 的另一個(gè)交點(diǎn)為
的另一個(gè)交點(diǎn)為![]() .
.
(i)求![]() 的半徑;
的半徑;
(ⅱ)連接![]() ,試探究
,試探究![]() 與
與![]() 的位置關(guān)系,并說(shuō)明理由.
的位置關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線![]() 經(jīng)過(guò)
經(jīng)過(guò)![]() ,
,![]()
![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,連接
,連接![]() 、
、![]() .
.
(1)![]() 與
與![]() 之間的關(guān)系式為: ;
之間的關(guān)系式為: ;
(2)判斷線段![]() 和
和![]() 之間的數(shù)量關(guān)系,并說(shuō)明理由;
之間的數(shù)量關(guān)系,并說(shuō)明理由;
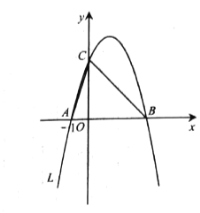
(3)設(shè)點(diǎn)![]() 是拋物線
是拋物線![]() 上
上![]() 、
、![]() 之間的動(dòng)點(diǎn),連接
之間的動(dòng)點(diǎn),連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí):
時(shí):
①若![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②若![]() ,且
,且![]() 的最大值為
的最大值為![]() ,請(qǐng)直接寫(xiě)出
,請(qǐng)直接寫(xiě)出![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
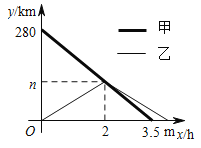
【題目】甲、乙兩車(chē)分別從![]() 兩地同時(shí)出發(fā),沿同一條公路相向行駛,相遇后,甲車(chē)?yán)^續(xù)以原速行駛到
兩地同時(shí)出發(fā),沿同一條公路相向行駛,相遇后,甲車(chē)?yán)^續(xù)以原速行駛到![]() 地,乙車(chē)立即以原速原路返回到
地,乙車(chē)立即以原速原路返回到![]() 地,甲、乙兩車(chē)距
地,甲、乙兩車(chē)距![]() 地的路程
地的路程![]() 與各自行駛的時(shí)間
與各自行駛的時(shí)間![]() 之間的關(guān)系如圖所示.
之間的關(guān)系如圖所示.
⑴![]() ________,
________,![]() ________;
________;
⑵求乙車(chē)距![]() 地的路程
地的路程![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并寫(xiě)出自變量
的函數(shù)解析式,并寫(xiě)出自變量![]() 的取值范圍;
的取值范圍;
⑶當(dāng)甲車(chē)到達(dá)![]() 地時(shí),求乙車(chē)距
地時(shí),求乙車(chē)距![]() 地的路程
地的路程
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
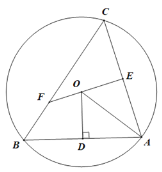
【題目】如圖所示,△ABC是圓O的內(nèi)接三角形,過(guò)點(diǎn)O作OD⊥AB與點(diǎn)D,連接OA,點(diǎn)E是AC的中點(diǎn),延長(zhǎng)EO交BC于點(diǎn)F.
(1)求證:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并說(shuō)明理由.
,△ABC是不是等腰三角形?并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】自行車(chē)因其便捷環(huán)保深受人們喜愛(ài),成為日常短途代步與健身運(yùn)動(dòng)首選.如圖1是某品牌自行車(chē)的實(shí)物圖,圖2是它的簡(jiǎn)化示意圖.經(jīng)測(cè)量,車(chē)輪的直徑為![]() ,中軸軸心
,中軸軸心![]() 到地面的距離
到地面的距離![]() 為
為![]() ,后輪中心
,后輪中心![]() 與中軸軸心
與中軸軸心![]() 連線與車(chē)架中立管
連線與車(chē)架中立管![]() 所成夾角
所成夾角![]() ,后輪切地面
,后輪切地面![]() 于點(diǎn)
于點(diǎn)![]() .為了使得車(chē)座
.為了使得車(chē)座![]() 到地面的距離
到地面的距離![]() 為
為![]() ,應(yīng)當(dāng)將車(chē)架中立管
,應(yīng)當(dāng)將車(chē)架中立管![]() 的長(zhǎng)設(shè)置為_____________
的長(zhǎng)設(shè)置為_____________![]() .
.
(參考數(shù)據(jù): ![]()
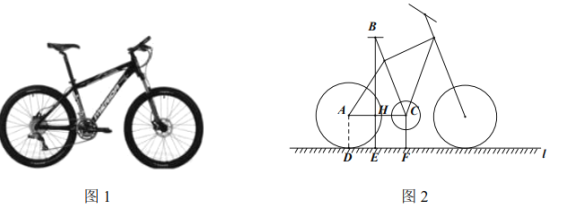
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com