Question

如圖，雙曲線經過的兩個頂點、軸，連接，將沿翻折后得到，點剛好落在線段上，連接，恰好平分與軸負半軸的夾角，若的面積為3，則的值為          。

Answer 1

-6.

解析試題分析：設BC的延長線交x軸于點D，連接OC，點C（-m，n），AB=a，由角平分線的性質得，CD=CB′，則△OCD≌△OCB′，再由翻折的性質得，BC=B′C，根據反比例函數的性質，可得出S_△OCD=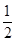mn=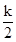，由AB∥x軸，得點A（a-m，2n），由題意得2n（a-m）=k，即可得出答案．
試題解析：如圖：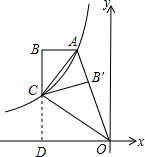

設BC的延長線交x軸于點D，
設點C（-m，n），AB=a，
∵∠ABC=90°，AB∥x軸，
∴CD⊥x軸，
由折疊的性質可得：∠AB′C=∠ABC=90°，
∴CB′⊥OA，
∵OC平分OA與x軸負半軸的夾角，
∴CD=CB′，
在Rt△OB′C和Rt△ODC中，
∵,
∴Rt△OCD≌Rt△OCB′（HL），
再由翻折的性質得，BC=B′C，
∴BC=CD，
∴點B（-m，2n）
∵雙曲線經過Rt△ABC的兩個頂點A、C,
∴S_△OCD=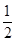|mn|=|k|
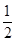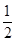∴mn=k
∵AB∥x軸，
∴點A（a-m，2n），
∴2n（a-m）=k
∴an=k
∴k=-6
考點: 反比例函數綜合題．