
【題目】如圖,直角梯形ABCO的兩邊OA,OC在坐標軸的正半軸上,BC∥x軸,OA=OC=4,以直線x=1為對稱軸的拋物線過A,B,C三點.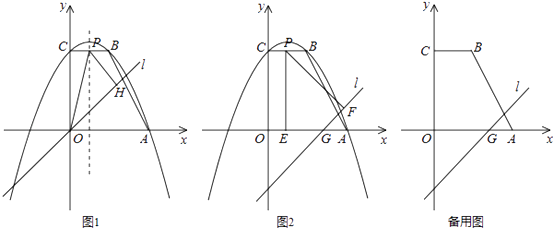
(1)求該拋物線的函數(shù)解析式;
(2)已知直線l的解析式為y=x+m,它與x軸交于點G,在梯形ABCO的一邊上取點P.
①當m=0時,如圖1,點P是拋物線對稱軸與BC的交點,過點P作PH⊥直線l于點H,連結OP,試求△OPH的面積;
②當m=﹣3時,過點P分別作x軸、直線l的垂線,垂足為點E,F(xiàn).是否存在這樣的點P,使以P,E,F(xiàn)為頂點的三角形是等腰三角形?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】
(1)
解:由題意得:A(4,0),C(0,4),對稱軸為x=1.
設拋物線的解析式為y=ax2+bx+c,則有:
 ,
,
解得  .
.
∴拋物線的函數(shù)解析式為:y=﹣ ![]() x2+x+4
x2+x+4
(2)
解:①當m=0時,直線l:y=x.
∵拋物線對稱軸為x=1,
∴CP=1.
如答圖1,延長HP交y軸于點M,則△OMH、△CMP均為等腰直角三角形.

∴CM=CP=1,
∴OM=OC+CM=5.
S△OPH=S△OMH﹣S△OMP= ![]() (
( ![]() OM)2﹣
OM)2﹣ ![]() OMCP=
OMCP= ![]() ×(
×( ![]() ×5)2﹣
×5)2﹣ ![]() ×5×1=
×5×1= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴S△OPH= ![]() .
.
②當m=﹣3時,直線l:y=x﹣3.
設直線l與x軸、y軸交于點G、點D,則G(3,0),D(0,﹣3).
假設存在滿足條件的點P.
(a)當點P在OC邊上時,如答圖2﹣1所示,此時點E與點O重合.

設PE=a(0<a≤4),
則PD=3+a,PF= ![]() PD=
PD= ![]() (3+a).
(3+a).
過點F作FN⊥y軸于點N,則FN=PN= ![]() PF,∴EN=|PN﹣PE|=|
PF,∴EN=|PN﹣PE|=| ![]() PF﹣PE|.
PF﹣PE|.
在Rt△EFN中,由勾股定理得:EF= ![]() =
= ![]() .
.
若PE=PF,則:a= ![]() (3+a),解得a=3(
(3+a),解得a=3( ![]() +1)>4,故此種情形不存在;
+1)>4,故此種情形不存在;
若PF=EF,則:PF= ![]() ,整理得PE=
,整理得PE= ![]() PF,即a=3+a,不成立,故此種情形不存在;
PF,即a=3+a,不成立,故此種情形不存在;
若PE=EF,則:PE= ![]() ,整理得PF=
,整理得PF= ![]() PE,即
PE,即 ![]() (3+a)=
(3+a)= ![]() a,解得a=3.
a,解得a=3.
∴P1(0,3).
(b)當點P在BC邊上時,如答圖2﹣2所示,此時PE=4.
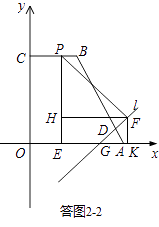
若PE=PF,則點P為∠OGD的角平分線與BC的交點,有GE=GF,過點F分別作FH⊥PE于點H,F(xiàn)K⊥x軸于點K,
∵∠OGD=135°,
∴∠EPF=45°,即△PHF為等腰直角三角形,
設GE=GF=t,則GK=FK=EH= ![]() t,
t,
∴PH=HF=EK=EG+GK=t+ ![]() t,
t,
∴PE=PH+EH=t+ ![]() t+
t+ ![]() t=4,
t=4,
解得t=4 ![]() ﹣4,
﹣4,
則OE=3﹣t=7﹣4 ![]() ,
,
∴P2(7﹣4 ![]() ,4)
,4)
(c)∵A(4,0),B(2,4),
∴可求得直線AB解析式為:y=﹣2x+8;
聯(lián)立y=﹣2x+8與y=x﹣3,解得x= ![]() ,y=
,y= ![]() .
.
設直線BA與直線l交于點K,則K( ![]() ,
, ![]() ).
).
當點P在線段BK上時,如答圖2﹣3所示.

設P(a,8﹣2a)(2≤a≤ ![]() ),則Q(a,a﹣3),
),則Q(a,a﹣3),
∴PE=8﹣2a,PQ=11﹣3a,
∴PF= ![]() (11﹣3a).
(11﹣3a).
與a)同理,可求得:EF= ![]() .
.
若PE=PF,則8﹣2a= ![]() (11﹣3a),解得a=1﹣2
(11﹣3a),解得a=1﹣2 ![]() <0,故此種情形不存在;
<0,故此種情形不存在;
若PF=EF,則PF= ![]() ,整理得PE=
,整理得PE= ![]() PF,即8﹣2a=
PF,即8﹣2a= ![]()
![]() (11﹣3a),解得a=3,符合條件,此時P3(3,2);
(11﹣3a),解得a=3,符合條件,此時P3(3,2);
若PE=EF,則PE= ![]() ,整理得PF=
,整理得PF= ![]() PE,即
PE,即 ![]() (11﹣3a)=
(11﹣3a)= ![]() (8﹣2a),解得a=5>
(8﹣2a),解得a=5> ![]() ,故此種情形不存在.
,故此種情形不存在.
(c)當點P在線段KA上時,如答圖2﹣4所示.
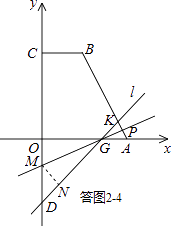
∵PE、PF夾角為135°,
∴只可能是PE=PF成立.
∴點P在∠KGA的平分線上.
設此角平分線與y軸交于點M,過點M作MN⊥直線l于點N,則OM=MN,MD= ![]() MN,
MN,
由OD=OM+MD=3,可求得M(0,3﹣3 ![]() ).
).
又因為G(3,0),
可求得直線MG的解析式為:y=( ![]() ﹣1)x+3﹣3
﹣1)x+3﹣3 ![]() .
.
聯(lián)立直線MG:y=( ![]() ﹣1)x+3﹣3
﹣1)x+3﹣3 ![]() 與直線AB:y=﹣2x+8,
與直線AB:y=﹣2x+8,
可求得:P4(1+2 ![]() ,6﹣4
,6﹣4 ![]() ).
).
(e)當點P在OA邊上時,此時PE=0,等腰三角形不存在.
綜上所述,存在滿足條件的點P,點P坐標為:(0,3)、(3,2)、(7﹣4 ![]() ,4)、(1+2
,4)、(1+2 ![]() ,6﹣4
,6﹣4 ![]() ).
).
【解析】(1)利用待定系數(shù)法求出拋物線的解析式;(2)①如答圖1,作輔助線,利用關系式S△OPH=S△OMH﹣S△OMP求解;②本問涉及復雜的分類討論,如答圖2所示.由于點P可能在OC、BC、BK、AK、OA上,而等腰三角形本身又有三種情形,故討論與計算的過程比較復雜,需要耐心細致、考慮全面.
【考點精析】掌握二次函數(shù)的性質(zhì)是解答本題的根本,需要知道增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知拋物線y=(x﹣m)2﹣(x﹣m),其中m是常數(shù).
(1)求證:不論m為何值,該拋物線與x軸一定有兩個公共點;
(2)若該拋物線的對稱軸為直線x= ![]() . ①求該拋物線的函數(shù)解析式;
. ①求該拋物線的函數(shù)解析式;
②把該拋物線沿y軸向上平移多少個單位長度后,得到的拋物線與x軸只有一個公共點.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某鎮(zhèn)水庫的可用水量為12000萬立方米,假設年降水量不變,能維持該鎮(zhèn)16萬人20年的用水量.實施城市化建設,新遷入4萬人后,水庫只夠維持居民15年的用水量.
(1)問:年降水量為多少萬立方米?每人年平均用水量多少立方米?
(2)政府號召節(jié)約用水,希望將水庫的保用年限提高到25年,則該鎮(zhèn)居民人均每年需節(jié)約多少立方米才能實現(xiàn)目標?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】將△ABC繞點A按逆時針方向旋轉(zhuǎn)θ度,并使各邊長變?yōu)樵瓉淼膎倍,得△AB′C′,即如圖①,我們將這種變換記為[θ,n].
(1)如圖①,對△ABC作變換[60°, ![]() ]得△AB′C′,則S△AB′C′:S△ABC=;直線BC與直線B′C′所夾的銳角為度;
]得△AB′C′,則S△AB′C′:S△ABC=;直線BC與直線B′C′所夾的銳角為度;
(2)如圖②,△ABC中,∠BAC=30°,∠ACB=90°,對△ABC 作變換[θ,n]得△AB′C′,使點B、C、C′在同一直線上,且四邊形ABB'C'為矩形,求θ和n的值;
(3)如圖③,△ABC中,AB=AC,∠BAC=36°,BC=1,對△ABC作變換[θ,n]得△AB′C′,使點B、C、B′在同一直線上,且四邊形ABB′C′為平行四邊形,求θ和n的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在四邊形ABCD中,∠DAB被對角線AC平分,且AC2=ABAD.我們稱該四邊形為“可分四邊形”,∠DAB稱為“可分角”.
(1)如圖2,在四邊形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求證:四邊形ABCD為“可分四邊形”;
(2)如圖3,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,如果∠DCB=∠DAB,則求∠DAB的度數(shù);
(3)現(xiàn)有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4,則△DAB的最大面積等于 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,AB=10cm,BC=6cm,AC=8cm,BD是∠ABC的角平分線。
(1)求△ABC的面積;
(2)求△ABC的角平分線BD的長;
(3)若點E是線段AB上的一個動點,從點B以每秒2cm的速度向A運動,幾秒種后△EAD是直角三角形?(此小題可直接寫出答案)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】九(3)班為了組隊參加學校舉行的“五水共治”知識競賽,在班里選取了若干名學生,分成人數(shù)相同的甲、乙兩組,進行了四次“五水共治”模擬競賽,成績優(yōu)秀的人數(shù)和優(yōu)秀率分別繪制成如圖統(tǒng)計圖. 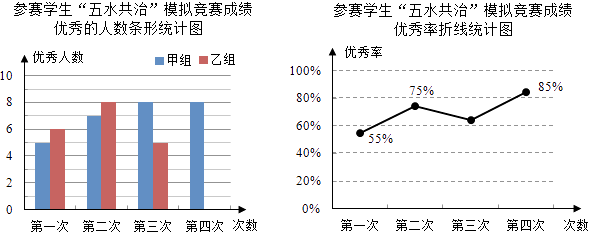
根據(jù)統(tǒng)計圖,解答下列問題:
(1)第三次成績的優(yōu)秀率是多少?并將條形統(tǒng)計圖補充完整;
(2)已求得甲組成績優(yōu)秀人數(shù)的平均數(shù) ![]() =7,方差
=7,方差 ![]() =1.5,請通過計算說明,哪一組成績優(yōu)秀的人數(shù)較穩(wěn)定?
=1.5,請通過計算說明,哪一組成績優(yōu)秀的人數(shù)較穩(wěn)定?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】射線QN與等邊△ABC的兩邊AB,BC分別交于點M,N,且AC∥QN,AM=MB=2cm,QM=4cm.動點P從點Q出發(fā),沿射線QN以每秒1cm的速度向右移動,經(jīng)過t秒,以點P為圓心, ![]() cm為半徑的圓與△ABC的邊相切(切點在邊上),請寫出t可取的一切值(單位:秒)
cm為半徑的圓與△ABC的邊相切(切點在邊上),請寫出t可取的一切值(單位:秒) 
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】△ABC在平面直角坐標系中的位置如圖所示.
(1)作△ABC關于原點O成中心對稱的△A1B1C1 .
(2)請寫出點B關于y軸對稱的點B2的坐標 . 若將點B2向下平移h單位,使其落在△A1B1C1內(nèi)部(不包括邊界),直接寫出h的值(寫出滿足的一個即可).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com