【題目】已知△ABC中，AB=20，AC=15，BC邊上的高為12，求△ABC的面積．
【答案】150或42．
【解析】分析：本題分兩種情況：∠B為銳角或∠C為鈍角已知AB、AC的值，利用勾股定理即可求出BC的長，再根據三角形的面積公式求解即可．
詳解：作AD⊥BC于D，則AD為BC邊上的高，AD=12．分兩種情況：
①高AD在三角形內，如圖1所示：在Rt△ADC中，由勾股定理得：
AC2=AD2+DC2，∴DC=9．在Rt△ADB中，由勾股定理得：
AB2=AD2+BD2，∴BD=16，∴BC=BD+DC=16+9=25，∴S△ABC=
×25×12=150；
②高AD在三角形外，如圖2所示：
在Rt△ADC中，由勾股定理得：
AC2=AD2+DC2
∴DC=9．在Rt△ADB中，由勾股定理得：
AB2=AD2+BD2，∴BD=16，∴BC=BD﹣DC=16﹣9=7，∴S△ABC=×7×12=42．
故答案為：150或42．
科目：初中數學 來源： 題型：
【題目】在數學的學習過程中，我們要善于觀察、發(fā)現規(guī)律并總結、應用．下面給同學們展示了四種有理數的簡便運算的方法：
方法①：（﹣
）2×162=[（﹣）×16]2=（﹣8）2=64，23×53=（2×5）3=103=1000
規(guī)律：a2b2=（ab）2，anbn=（ab）n （n為正整數）
方法②：3.14×23+3.14×17+3.14×60=3.14×（23+17+60）=3.14×100=314
規(guī)律：ma+mb+mc=m（a+b+c）
方法③：（﹣12
）÷3=[（﹣12）+（﹣）]×
=（﹣12）×+（﹣）×=（﹣4）+（﹣
）=﹣4
方法④：
=1﹣，
=﹣，
=﹣，
=﹣
，…
規(guī)律：
=
﹣
（n為正整數）
利用以上方法，進行簡便運算：
①（﹣0.125）2014×82014；
×（﹣
）﹣（﹣
）×（﹣）﹣×2
；
③（﹣20
）÷（﹣5）；
④+++…+
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=BC，以AB為直徑的⊙O交AC于點D，過D作直線DE垂直BC于F，且交BA的延長線于點E．
（1）求證：直線DE是⊙O的切線；
（2）若cos∠BAC= 
，⊙O的半徑為6，求線段CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，動點P在平面直角坐標系中按圖中箭頭所示方向運動，第1次從原點運動到點（1，1），第2次接著運動到點（2，0），第3次接著運動到點（3，2），…，按這樣的運動規(guī)律，經過第2016次運動后，動點P的坐標是（ ）
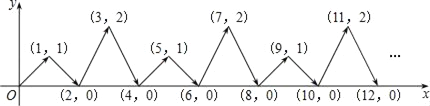
A. （2016，1） B. （2016，0） C. （2016，2） D. （2017，0）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某數學小組的10位同學站成一列做報數游戲，規(guī)則是：從前面第一位同學開始，每位同學依次報自己順序的倒數的2倍加1，第1位同學報 
，第2位同學報 
，第3位同學報 
，…這樣得到10個數的積為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是正方形，其中A（1，1），B（3，1），D（1，3）．反比例函數 
的圖象經過對角線BD的中點M，與BC，CD的邊分別交于點P、Q．
（1）直接寫出點M，C的坐標；
（2）求直線BD的解析式；
（3）線段PQ與BD是否平行？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知一次函數y=﹣ 
x+b的圖象經過點A（2，3），AB⊥x軸，垂足為B，連接OA．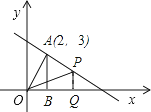 
（1）求此一次函數的解析式；
（2）設點P為直線y=﹣ x+b上的一點，且在第一象限內，經過P作x軸的垂線，垂足為Q．若S△POQ= 
S△AOB ， 求點P的坐標．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
