
【題目】在小學,我們已經初步了解到,正方形的每個角都是90°,每條邊都相等.如圖,在正方形ABCD外側作直線AQ,且∠QAD=30°,點D關于直線AQ的對稱點為E,連接DE、BE,DE交AQ于點G,BE交AQ于點F.
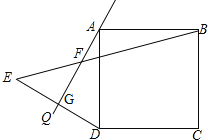
(1)求∠ABE的度數;
(2)若AB=6,求FG的長.
【答案】(1)15°;(2)3
【解析】
試題分析:(1)連接AE,由軸對稱的性質和線段垂直平分線的性質得出∠EAQ=∠QAD=30°,由正方形的性質得出∠BAD=90°,AB=AD,得出AE=AB,由等腰三角形的性質和三角形內角和定理即可得出結果;
(2)證出△AED是等邊三角形,得出ED=6,由線段垂直平分線得出EG=3,∠FGE=90°,證出∠EFG=∠FEG=45°,得出EG=FG=3即可.
解:(1)連接AE,如圖1所示:

∵點D關于直線AQ的對稱點為E,
∴AE=AD,AQ垂直平分DE,
∴∠EAQ=∠QAD=30°,
∵四邊形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∴AE=AB,
∴∠BAE=30°+30°+90°=150°,
∴∠ABE=![]() (180°﹣150°)=15°;
(180°﹣150°)=15°;
(2)由(1)得:AE=AD,∠EAD=60°,
∴△AED是等邊三角形,ED=6,
∵AQ垂直平分DE,
∴EG=3,∠FGE=90°,
∵∠EAD=30°,∠AEB=15°,
∴∠EFG=∠FEG=45°,
∴EG=FG=3.


科目:初中數學 來源: 題型:
【題目】我們把一個半圓與二次函數圖象的一部分合成的封閉圖形稱為“蛋圓”,如果一條直線與“蛋圓”只有一個交點(半圓與二次函數圖象的連接點除外),那么這條直線叫做“蛋圓”的切線.如圖,二次函數y=x2﹣2x﹣3的圖象與x軸交于點A、B,與y軸交于點D,AB為半圓直徑,半圓圓心為點M,半圓與y軸的正半軸交于點C.
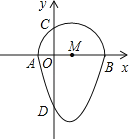
(1)求點C的坐標;
(2)分別求出經過點C和點D的“蛋圓”的切線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一副三角尺ABC與BDE按如圖所示那樣拼在一起,其中A、B、D三點在同一直線上,BM為∠CBE的平分線,BN為∠DBE的平分線,則∠MBN的度數是( )
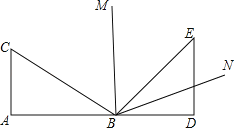
A.60° B.67.5° C.75° D.85°
查看答案和解析>>
科目:初中數學 來源: 題型:
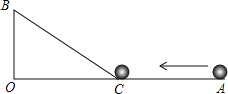
【題目】如圖,∠AOB=90°,OA=9cm,OB=3cm,一機器人在點B處看見一個小球從點A出發沿著AO方向勻速滾向點O,機器人立即從點B出發,沿BC方向勻速前進攔截小球,恰好在點C處截住了小球.如果小球滾動的速度與機器人行走的速度相等,那么機器人行走的路程BC是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年,深圳市人居環境委通報了2014年深圳市大氣PM2.5來源研究成果.報告顯示主要來源有,A:機動車尾氣,B:工業VOC轉化及其他工業過程,C:揚塵,D:遠洋船,E:電廠,F:其它.某教學學習小組根據這些數據繪制出了如下兩幅尚不完整的統計圖(圖1,圖2).
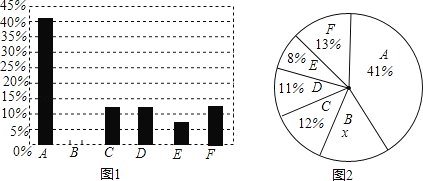
請你根據統計圖中所提供的信息解答下列問題:
(1)圖2的扇形統計圖中,x的值是 ;
(2)請補全圖1中的條形統計圖;
(3)圖2的扇形統計圖中,“A:機動車尾氣”所在扇形的圓心角度數為 度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB,CD相交于點O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度數;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com