
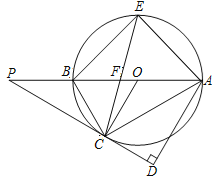
【題目】如圖所示,AB是⊙O的直徑,P為AB延長線上的一點(diǎn),PC切⊙O于點(diǎn)C,AD⊥PC,垂足為D,弦CE平分∠ACB,交AB于點(diǎn)F,連接AE.
(1)求證:∠CAB=∠CAD;
(2)求證:PC=PF;
(3)若tan∠ABC=![]() ,AE=5
,AE=5![]() ,求線段PC的長.
,求線段PC的長.
【答案】(1)見解析;(2)見解析;(3)12.
【解析】
(1)由切線得:OC⊥PC,再得平行,由同圓的半徑相等:OA=OC,根據(jù)等邊對等角可得結(jié)論;
(2)證明∠PFC=∠PCF,根據(jù)等角對等邊可得結(jié)論;
(3)根據(jù)三角函數(shù)的比設(shè)未知數(shù),利用勾股定理列方程可得結(jié)論.
(1)證明:∵PC為⊙O的切線,
∴OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠OAC,
∴AC平分∠DAB;
(2)證明:∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴![]() ,
,
∴∠ABE=∠ECB,
∵∠BCP+∠OCB=∠BCP+∠OBC=∠BAC+∠OBC=90°,
∴∠BCP=∠BAC,
∵∠BAC=∠BEC,
∴∠BCP=∠BEC,
∵∠PFC=∠BEC+∠ABE,
∠PCF=∠ECB+∠BCP,
∴∠PFC=∠PCF,
∴PC=PF;
(3)解:∵![]() ,
,
∴AE=BE=5![]() ,
,
又∵AB是直徑,
∴∠AEB=90°,
AB=![]() BE=10,
BE=10,
∴OB=OC=5,
∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC,
∴![]() ,
,
∵tan∠ABC=![]() ,
,
∴![]() ,
,
設(shè)PB=2x,則PC=3x,
在Rt△POC中,(2x+5)2=(3x)2+52,
解得x1=0(舍),x2=4,
∵x>0,
∴x=4,
∴PC=3x=3×4=12.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
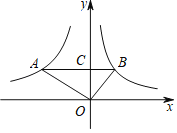
【題目】如圖,A,B分別在反比例函數(shù)![]() (x<0)和
(x<0)和![]() (x>0)的圖象上,AB∥x軸,交y軸于點(diǎn)C.若△AOC的面積是△BOC面積的2倍.
(x>0)的圖象上,AB∥x軸,交y軸于點(diǎn)C.若△AOC的面積是△BOC面積的2倍.
(1)求k的值;
(2)當(dāng)∠AOB=90°時,直接寫出點(diǎn)A,B的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形ABCD中,AB=6,AD=8,點(diǎn)E是邊AD上一點(diǎn),EM⊥BC交AB于點(diǎn)M,點(diǎn)N在射線MB上,且AE是AM和AN的比例中項(xiàng).
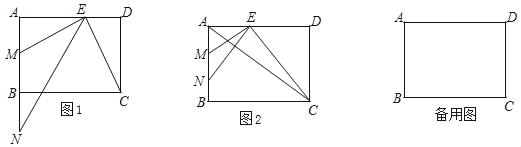
(1)如圖1,求證:∠ANE=∠DCE;
(2)如圖2,當(dāng)點(diǎn)N在線段MB之間,聯(lián)結(jié)AC,且AC與NE互相垂直,求MN的長;
(3)連接AC,如果△AEC與以點(diǎn)E、M、N為頂點(diǎn)所組成的三角形相似,求DE的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,是一座古拱橋的截面圖,拱橋橋洞的上沿是拋物線形狀,當(dāng)水面的寬度為10m時,橋洞與水面
的最大距離是5m.
(1)經(jīng)過討論,同學(xué)們得出三種建立平面直角坐標(biāo)系的方案(如下圖)
你選擇的方案是_____(填方案一,方案二,或方案三),則B點(diǎn)坐標(biāo)是______,求出你所選方案中的拋物線的表達(dá)式;
(2)因?yàn)樯嫌嗡畮煨购?/span>,水面寬度變?yōu)?/span>6m,求水面上漲的高度.


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將含有30°角的直角三角板ABC放入平面直角坐標(biāo)系,頂點(diǎn)A,B分別落在x、y軸的正半軸上,∠OAB=60°,點(diǎn)A的坐標(biāo)為(1,0),將三角板ABC沿x軸向右作無滑動的滾動(先繞點(diǎn)A按順時針方向旋轉(zhuǎn)60°,再繞點(diǎn)C按順時針方向旋轉(zhuǎn)90°,…)當(dāng)點(diǎn)B第一次落在x軸上時,則點(diǎn)B運(yùn)動的路徑與坐標(biāo)軸圍成的圖形面積是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的外角∠EAC的平分線AD交其外接圓⊙O于點(diǎn)D,連接DB,DC.
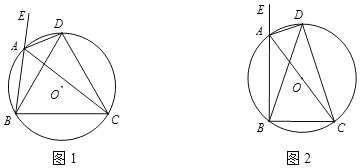
(1)如圖1,求證BD=CD;
(2)如圖2,若AC是⊙O的直徑,sin∠BDC=![]() ,求tan∠DBA的值.
,求tan∠DBA的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】隨著交通道路的不斷完善,帶動了旅游業(yè)的發(fā)展,某市旅游景區(qū)有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等著名景點(diǎn),該市旅游部門統(tǒng)計(jì)繪制出2019年“五·一”長假期間旅游情況統(tǒng)計(jì)圖,根據(jù)以下信息解答下列問題:
等著名景點(diǎn),該市旅游部門統(tǒng)計(jì)繪制出2019年“五·一”長假期間旅游情況統(tǒng)計(jì)圖,根據(jù)以下信息解答下列問題:

(1)扇形統(tǒng)計(jì)圖中![]() 景點(diǎn)所對應(yīng)的圓心角的度數(shù)是______;
景點(diǎn)所對應(yīng)的圓心角的度數(shù)是______;
(2)請補(bǔ)全條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖;
(3)根據(jù)近幾年到該市旅游人數(shù)增長趨勢,預(yù)計(jì)2020年“五·一”節(jié)將有80萬游客選擇該市旅游,請估計(jì)有多少萬人會選擇去![]() 景點(diǎn)旅游?
景點(diǎn)旅游?
(4)甲,乙兩個旅行團(tuán)在![]() ,
,![]() ,
,![]() 三個景點(diǎn)中,同時選擇去同一景點(diǎn)的概率是多少?請用畫樹狀圖或列表法加以說明.
三個景點(diǎn)中,同時選擇去同一景點(diǎn)的概率是多少?請用畫樹狀圖或列表法加以說明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中AC,BD相交于點(diǎn)O,點(diǎn)E是OA的中點(diǎn),連接BE并延長AD于點(diǎn)F,已知△AEF的面積=1,則平行四邊形ABCD的面積是( )
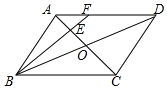
A.24B.18C.12D.9
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
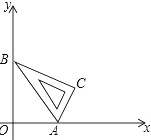
【題目】如圖,△ABC的三個頂點(diǎn)和點(diǎn)O都在正方形網(wǎng)格的格點(diǎn)上,每個小正方形的邊長都為1.
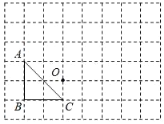
(1)將△ABC先向右平移4個單位,再向上平移2個單位得到△A1B1C1,請畫出△A1B1C1;
(2)請畫出△A2B2C2,使△A2B2C2和△ABC關(guān)于點(diǎn)O成中心對稱.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com