
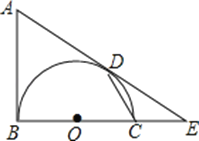
【題目】如圖,AB是以BC為直徑的半圓O的切線,D為半圓上一點,AD=AB,AD,BC的延長線相交于點E.
(1)求證:AD是半圓O的切線;
(2)連結CD,求證:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的長.
的長.
【答案】(1)證明見解析;(2)證明見解析;(3)![]()
【解析】試題分析:(1)連接OD,BD,根據圓周角定理得到∠ABO=90°,根據等腰三角形的性質得到∠ABD=∠ADB,∠DBO=∠BDO,根據等式的性質得到∠ADO=∠ABO=90°,根據切線的判定定理即可得到即可;
(2)由AD是半圓O的切線得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根據圓周角定理得到∠ODC+∠BDO=90°,等量代換得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到結論;
(3)根據已知條件得到∠DOC=2∠CDE=54°,根據平角的定義得到∠BOD=180°-54°=126°,然后由弧長的公式即可計算出結果.
試題解析:(1)連接OD,BD,
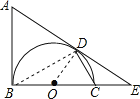
∵AB是⊙O的切線,∴AB⊥BC,即∠ABO=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°;
又∵OD是圓O的半徑,∴AD是半圓O的切線;
(2)證明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠COD
∵AD是半圓O的切線,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直徑,∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO=2∠CDE,
∴∠A=2∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°,
∵OB=2,∴![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,對角線AC,BD交于O,EO⊥AC, 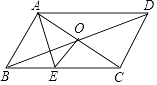
(1)若△ABE的周長為10cm,求平行四邊形ABCD的周長,
(2)若∠DAB=108°,AE平分∠BAC,試求∠ACB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】人體中紅細胞的直徑約為0.0000077米,將0.0000077用科學記數法表示為( )
A.7.7×10﹣6B.7.7×10﹣5C.0.77×10﹣6D.0.77×10﹣5
查看答案和解析>>
科目:初中數學 來源: 題型:
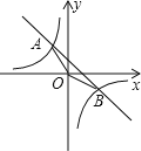
【題目】如圖,已知一次函數y=kx+b的圖象與反比例函數![]() 的圖象交于A,B兩點,且點A的橫坐標和點B的縱坐標都是﹣2,
的圖象交于A,B兩點,且點A的橫坐標和點B的縱坐標都是﹣2,
求:(1)一次函數的解析式;
(2)△AOB的面積;
(3)直接寫出一次函數的函數值大于反比例函數的函數值時x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),
…,
M(n)= ![]() .
.
(1)計算:M(5)+M(6);
(2)求2M(2 016)+M(2 017)的值;
(3)說明2M(n)與M(n+1)互為相反數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:求1+2+22+23+24+…+22 015+22 016的值.
解:設S=1+2+22+23+24+…+22 015+22 016, ①
將等式兩邊同時乘2,得2S=2+22+23+24+25+…+22 016+22 017, ②
②-①,得2S-S=22 017-1,即S=22 017-1,
所以1+2+22+23+24+…+22 015+22 016=22 017-1.
請你仿照此法計算:
(1)1+2+22+23+24+…+29+210;
(2)1+3+32+33+34+…+3n-1+3n(其中n為正整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB,CD相交于點O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度數;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,(10分)AB∥DE,試問∠B、∠E、∠BCE有什么關系.

解:∠B+∠E=∠BCE
過點C作CF∥AB,
則![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com