
【題目】如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H,給出下列結論:①![]() ;②△DFP△BPH;③
;②△DFP△BPH;③![]() ; ④
; ④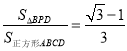 .其中正確的是______.(寫出所有正確結論的序號).
.其中正確的是______.(寫出所有正確結論的序號).
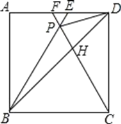
【答案】②③
【解析】
依據∠FDP=∠PBD,∠DFP=∠BPC=60°,即可得到△DFP∽△BPH,![]() ,判定△DPH∽△CPD,可得
,判定△DPH∽△CPD,可得![]() ,即PD2=PHCP,再根據CP=CD,即可得出PD2=PHCD;根據三角形面積計算公式,結合圖形得到△BPD的面積=△BCP的面積+△CDP面積-△BCD的面積,即可得出
,即PD2=PHCP,再根據CP=CD,即可得出PD2=PHCD;根據三角形面積計算公式,結合圖形得到△BPD的面積=△BCP的面積+△CDP面積-△BCD的面積,即可得出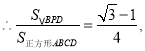
解:∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,故②正確;
∴![]()
故①不正確;
∵PC=DC,∠DCP=30°,
∴∠CDP=75°,
又∵∠DHP=∠DCH+∠CDH=75°,
∴∠DHP=∠CDP,而∠DPH=∠CPD,
∴△DPH∽△CPD,
∴![]() ,即PD2=PHCP,
,即PD2=PHCP,
又∵CP=CD,
∴PD2=PHCD,故③正確;
如圖,過P作PM⊥CD,PN⊥BC,
設正方形ABCD的邊長是4,△BPC為正三角形,則正方形ABCD的面積為16,
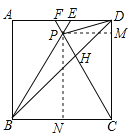
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
![]()
![]()
![]()
![]()
![]()
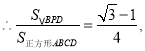 故④錯誤;
故④錯誤;
故答案為:②③


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() ,
,![]() ,
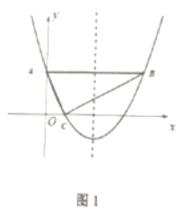
,![]() 軸,如圖1,
軸,如圖1,![]() ,且
,且![]()
![]() .
.
(1)![]() 點坐標為__________,
點坐標為__________,![]() 點坐標為__________;
點坐標為__________;
(2)求過![]() 、
、![]() 、
、![]() 三點的拋物線表達式;
三點的拋物線表達式;
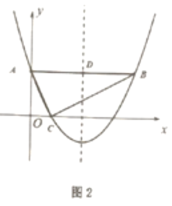
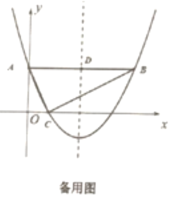
(3)如圖2,拋物線對稱軸與![]() 交于點
交于點![]() ,現有一點
,現有一點![]() 從點
從點![]() 出發,以每秒1個單位的速度在
出發,以每秒1個單位的速度在![]() 上向點
上向點![]() 運動,另一點
運動,另一點![]() 從點
從點![]() 與點
與點![]() 同時出發,以每秒5個單位在拋物線對稱軸上運動.當點
同時出發,以每秒5個單位在拋物線對稱軸上運動.當點![]() 到達
到達![]() 點時,點
點時,點![]() 、
、![]() 同時停止運動,問點
同時停止運動,問點![]() 、
、![]() 運動到何處時,
運動到何處時,![]() 面積最大,試求出最大面積.
面積最大,試求出最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家衛生健康委員會公布,截止4月2日全國疫情現存趨勢圖如下:

(1)結合圖象,小彤對全國疫情做出以下四個判斷:
①現存疑似病例與現存確診病例數量差距最大日期大約出現在2月上旬;
②疫情在3月30日已經得到完全的控制;
③現存疑似人數大約在2月8日前后達到峰值;
④全國現存確診病例人數3月底增加趨緩.
你認為判斷正確的有________.
(2)針對這次疫情,某校初三一班的同學以小組為單位組織了“抗戰疫情,我為湖北鼓勁”繪畫活動.通過網絡發往湖北,右圖是同學們的上交繪畫作品情況,結合統計圖,回答:![]() ________,
________,![]() ________.
________.

(3)全國各地都向湖北伸出援助之手,其中北京市派遣醫務人員前往較為嚴重的武漢和黃岡.請依據表格回答下列問題:
北京派遣至武漢、黃岡各醫院醫護人員對比表 | ||||||
武漢 | ||||||
5 | 7 | 9 | 12 | 11 | 8 | 19 |
20 | 7 | 7 | 3 | 1 | 20 | 13 |
黃岡 | ||||||
3 | 8 | 5 | 10 | 14 | 20 | |
4 | 2 | 9 | 18 | 11 | 15 | |
注:表格內的數字代表派遣至每個醫院的醫護人員人數 | ||||||
①派往武漢各醫院醫護人員的眾數是________人;
②派黃岡各醫院醫護人員的平均數約是________人(四舍五入取整數);
③請你根據表格信息,判斷兩個地區哪里的疫情較為嚴重,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BCA=90°,CD是邊AB上的中線,分別過點C,D作BA和BC的平行線,兩線交于點E,且DE交AC于點O,連接AE.

(1)求證:四邊形ADCE是菱形;
(2)若∠B=60°,BC=6,求四邊形ADCE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某駐村扶貧小組實施產業扶貧,幫助貧困農戶進行西瓜種植和銷售.已知西瓜的成本為6元/千克,規定銷售單價不低于成本,又不高于成本的兩倍.經過市場調查發現,某天西瓜的銷售量y(千克)與銷售單價x(元/千克)的函數關系如下圖所示:
(1)求y與x的函數解析式(也稱關系式);
(2)求這一天銷售西瓜獲得的利潤的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2022年在北京將舉辦第24屆冬季奧運會,很多學校都開展了冰雪項目學習.如圖,滑雪軌道由AB、BC兩部分組成,AB、BC的長度都為200米,一位同學乘滑雪板沿此軌道由A點滑到了C點,若AB與水平面的夾角α為20°,BC與水平面的夾角β為45°,則他下降的高度為___________米(精確到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
科目:初中數學 來源: 題型:
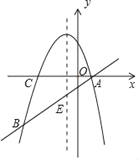
【題目】如圖,拋物線y=ax2+bx+3(a≠0)的對稱軸為直線x=﹣1,拋物線交x軸于A、C兩點,與直線y=x﹣1交于A、B兩點,直線AB與拋物線的對稱軸交于點E.
(1)求拋物線的解板式.
(2)點P在直線AB上方的拋物線上運動,若△ABP的面積最大,求此時點P的坐標.
(3)在平面直角坐標系中,以點B、E、C、D為頂點的四邊形是平行四邊形,請直接寫出符合條件點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠生產某種產品,每件產品的出廠價為50元,成本為25元.由于在生產過程中,平均每生產1件產品,有![]() 污水排出,所以為了凈化環境,工廠設計兩種方案對污水進行處理,并準備實施.
污水排出,所以為了凈化環境,工廠設計兩種方案對污水進行處理,并準備實施.
方案甲:工廠將污水排到污水廠統一處理,每處理![]() 需付14元的排污費;
需付14元的排污費;
方案乙:工廠將污水進行凈化處理后再排出,每處理![]() 污水所用原料費為2元,且每月凈化設備的損耗費為30000元.設工廠每月生產x件產品(x為正整數,
污水所用原料費為2元,且每月凈化設備的損耗費為30000元.設工廠每月生產x件產品(x為正整數,![]() ).
).
(1)根據題意填寫下表:
每月生產產品的數量/件 | 3500 | 4500 | 5500 | … |
方案甲處理污水的費用/元 | 31500 | … | ||
方案乙處理污水的費用/元 | 34500 | … |
(2)設工廠按方案甲處理污水時每月獲得的利潤為![]() 元,按方案乙處理污水時每月獲得的利潤為
元,按方案乙處理污水時每月獲得的利潤為![]() 元,分別求
元,分別求![]() ,
,![]() 關于x的函數解析式;
關于x的函數解析式;
(3)根據題意填空:
①若該工廠按方案甲處理污水時每月獲得的利潤和按方案乙處理污水時每月獲得利潤相同,則該工廠每月生產產品的數量為_______件;
②若該工廠每月生產產品的數量為7500件時,則該工廠選用方案甲、方案乙中的方案_______處理污水時所獲得的利潤多;
③若該工廠每月獲得的利潤為81000元,則該工廠選用方案甲、方案乙中的方案________處理污水時生產產品的數量少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com