
���}Ŀ����֪����D����Rt��ABC�У���C=90����AD�ǡ�ABC�Ľ�ƽ�־���DE��AB��������c(di��n)E��AE=BE.
(1)���룺��B�ĶȔ�(sh��)�����C����IJ���.
(2)���AC=3cm��CD=2cm�����ABD����e.

���𰸡�(1)��B=30�����C��Ҋ������(2)S��ABD=6cm2.
��������
(1)����(j��)��֪�l���õ�AD=BD���ɵ��������ε����|(zh��)�õ���B=��DAE������(j��)AD�ǡ�ABC�Ľ�ƽ�־�����á�DAE=��DAC�����ǵõ���B=��DAE=��DAC���з��̼��ɵõ��Y(ji��)Փ��
(2)����(j��)��֪�l�����Rt��ACD��Rt��AED������(j��)ȫ�������ε����|(zh��)�õ�AE=BE�����ǵõ�AB=2AE=2��3=6�����ɵõ��Y(ji��)Փ.
�⣺(1)���룺��B=30����
��DE��AB��AE=BE��
��AD=BD��
���B=��DAE��
��AD�ǡ�ABC�Ľ�ƽ�־���
���DAE=��DAC��
���B=��DAE=��DAC��
�ߡ�C=90����
���B+��DAE+��DAC=90����
���B=30����
(2)�ߡ�C=90����AD�ǡ�ABC�Ľ�ƽ�־���DE��AB��
��Rt��ACD��Rt��AED��
��AE=BE��
��AB=2AE=2��3=6��
��S��ABD=![]() ABDE=
ABDE=![]() ��6��2=6cm2.
��6��2=6cm2.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������x������ս��}��
�ٷ���x2��x��6=0�ĸ���x1=3��x2=��2���tx1+x2=1��x1x2=��6��
�ڷ���2x2��7x+3=0�ĸ���x1=![]() ��x2=3���tx1+x2=
��x2=3���tx1+x2=![]() ��x1x2=
��x1x2=![]() ��
��
����(j��)���Ϣ٢����ܷ�³���
����P(gu��n)��x��һԪ���η���ax2+bx+c=0��a��0����a��b��c�鳣��(sh��)��b2��4ac��0���Ѓɸ�x1��x2����ôx1+x2��x1x2�cϵ��(sh��)a��b��c��ʲô�P(gu��n)ϵ��Ո������IJ��벢�f�����ɣ�
���ù�ʽ��������̵ĸ����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��C����A�ص����|�������д�ɽ�������A�ص�C����Ҫ�@�и�����B�أ���֪B��λ��A�صı�ƫ�|67�������xA��520km��C��λ��B����ƫ��30��������Ҫ��ͨ��ɽ���������F����AC���L���Y(ji��)����������(sh��)����������(sh��)��(j��)��![]() ��1.73��sin67���
��1.73��sin67���![]() ��cos67���
��cos67���![]() ��tan67���
��tan67���![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У�![]() ��
��![]() �ҝM�㣺
�ҝM�㣺![]() ���L����
���L����![]() ������(bi��o)ϵ�У���D1�����c(di��n)
������(bi��o)ϵ�У���D1�����c(di��n)![]() ������(bi��o)ϵ��ԭ�c(di��n)��
������(bi��o)ϵ��ԭ�c(di��n)��

��1�����c(di��n)![]() ������(bi��o)��
������(bi��o)��
��2����D2�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ���l(f��)����2����λ/����ٶ������\(y��n)�ӣ������^�c(di��n)
���l(f��)����2����λ/����ٶ������\(y��n)�ӣ������^�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ��ԭ�c(di��n)
��ԭ�c(di��n)![]() ���l(f��)����1����λ/����ٶ������\(y��n)�ӣ������^�c(di��n)
���l(f��)����1����λ/����ٶ������\(y��n)�ӣ������^�c(di��n)![]() �����O(sh��)
�����O(sh��)![]() ���c(di��n)ͬ�r���l(f��)���������\(y��n)�ӵ��^���У���߅��
���c(di��n)ͬ�r���l(f��)���������\(y��n)�ӵ��^���У���߅��![]() ����e�Ƿ�l(f��)��׃��������׃������ֵ����׃������׃���ķ�����
����e�Ƿ�l(f��)��׃��������׃������ֵ����׃������׃���ķ�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���nj�����ABCD���c(di��n)O�����İ�형rᘷ���քe���D(zhu��n)90�㣬180�㣬270����γɵĈD�Σ�����BAD=60�㣬AB=2���t�D���Ӱ���ֵ���e���� ����

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
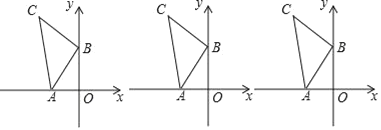
���}Ŀ����D��A(m��0)��B(0��n)����B�c(di��n)��ֱ����c(di��n)�ڵڶ�����������ֱ�ǡ�ABC.
(1)��C�c(di��n)������(bi��o).
(2)��y�S�҂�(c��)��ƽ���(n��i)�Ƿ����һ�c(di��n)P��ʹ��PAB�c��ABCȫ�ȣ������ڣ����P�c(di��n)����(bi��o)���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������εăɂ���(n��i)��![]() ��
��![]() �M��
�M��![]() ����ô�҂��Q�@�ӵ������О顰��(zh��n)ֱ�������Ρ���
����ô�҂��Q�@�ӵ������О顰��(zh��n)ֱ�������Ρ���
��1����D�٣���![]() �У�
��![]() ��
��![]() ��
��![]() �Ľ�ƽ�־���
�Ľ�ƽ�־���
���C��![]() �ǡ���(zh��n)ֱ�������Ρ���
�ǡ���(zh��n)ֱ�������Ρ���


��2���P(gu��n)�ڡ���(zh��n)ֱ�������Ρ��������f����
����![]() ����
����![]() ���t
���t![]() �ǜ�(zh��n)ֱ�������Σ�
�ǜ�(zh��n)ֱ�������Σ�
����![]() �ǡ���(zh��n)ֱ�������Ρ���
�ǡ���(zh��n)ֱ�������Ρ���![]() ���t
���t![]() ��
��
�ۡ���(zh��n)ֱ�������Ρ�һ�����g�������Σ����У����_���� ������������_�Y(ji��)Փ����̖��
��3����D�ڣ�![]() ��ֱ��
��ֱ��![]() �σ��c(di��n)���c(di��n)
�σ��c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �⣬��
�⣬��![]() ����
����![]() ��
��![]() ��һ�c(di��n)����
��һ�c(di��n)����![]() ������(zh��n)ֱ�������Ρ���Ոֱ������
������(zh��n)ֱ�������Ρ���Ոֱ������![]() �ĶȔ�(sh��)��
�ĶȔ�(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D�����タy=x2+bx+c�cx�S����A��-1��0����B��3��0�����c(di��n)��

��1����ԓ���タ�Ľ���ʽ��
��2����ԓ���タ�Č��Q�S�Լ���c(di��n)����(bi��o)��
��3���O(sh��)��1���еĒ��タ����һ�����c(di��n)P����(d��ng)�c(di��n)P��ԓ���タ�ϻ��ӵ�ʲôλ�Õr���M��S��PAB=8��������˕rP�c(di��n)������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1��OABC��߅OC��y�S�������S�ϣ�![]() ��
��![]() ������������(sh��)
������������(sh��)![]() �ĈD��(j��ng)�^��B��
�ĈD��(j��ng)�^��B��

![]() ���c(di��n)B������(bi��o)�ͷ���������(sh��)���P(gu��n)ϵʽ��
���c(di��n)B������(bi��o)�ͷ���������(sh��)���P(gu��n)ϵʽ��
![]() ��D2��ֱ��MN�քe�cx�S��y�S�������S����M��N���c(di��n)�����c(di��n)O���c(di��n)B�P(gu��n)��ֱ��MN���S���Q����ON���L��
��D2��ֱ��MN�քe�cx�S��y�S�������S����M��N���c(di��n)�����c(di��n)O���c(di��n)B�P(gu��n)��ֱ��MN���S���Q����ON���L��
![]() ��D3��������OA���L��
��D3��������OA���L��![]() �ĈD�����c(di��n)D���^B��D��ֱ���քe��x�S��y�S��E��F���c(di��n)��Ո?zh��)�������ED�cBF�Ĕ�(sh��)���P(gu��n)ϵ�����f�����ɣ�
�ĈD�����c(di��n)D���^B��D��ֱ���քe��x�S��y�S��E��F���c(di��n)��Ո?zh��)�������ED�cBF�Ĕ�(sh��)���P(gu��n)ϵ�����f�����ɣ�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com