
【題目】![]() 中,
中,![]() ,
,![]() 的頂點
的頂點![]() 是底邊
是底邊![]() 的中點,兩邊分別與
的中點,兩邊分別與![]() 交于點
交于點![]() .
.
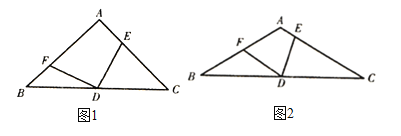
(1)如圖1,![]() ,當
,當![]() 的位置變化時,
的位置變化時,![]() 是否隨之變化?證明你的結論;
是否隨之變化?證明你的結論;
(2)如圖2,當![]() ,當
,當![]() °時,(1)中的結論仍然成立,求出此時
°時,(1)中的結論仍然成立,求出此時![]() 的值.
的值.
【答案】(1)BF+CE=a,是定值,不變.見解析;(2)60,9
【解析】
(1)結論:BF+CE=a,是定值.如圖1中,連接AD.只要證明△BDF≌△ADE即可解決問題;
(2)當∠EDF=60°時,BF+EC=9,是定值.連接AD,作DM⊥AB于M,DN⊥AC于N.只要證明△DMF≌△DNE(ASA),推出FM=EN,由含30°的直角三角形的性質,推出BM=CN=![]() ,推出BF+CE=BMFM+CN+EN=2BM,即可解決問題.
,推出BF+CE=BMFM+CN+EN=2BM,即可解決問題.
解:(1)結論:BF+CE=a,是定值.
理由:如圖1中,連接AD.
∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥BC,∠B=∠C=∠BAD=∠CAD=45°,AD=BD=CD.
∵∠EDF=∠ADB=90°,
∴∠BDF=∠ADE,
∴△BDF≌△ADE(ASA),
∴BF=AE,
∴BF+CE=AE+CE=AC=a,是定值.
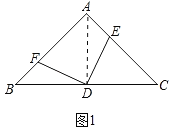
(2)當∠EDF=60°時,BF+EC=9,是定值.
理由:如圖2中,連接AD,作DM⊥AB于M,DN⊥AC于N.
∵∠AMD=∠AND=90°,∠A=120°,
∴∠MDN=∠EDF=60°,
∴∠MDF=∠NDE,
∵AB=AC,BD=CD,
∴∠BAD=∠CAD,
∵DM⊥AB于M,DN⊥AC于N,
∴DM=DN,
∴△DMF≌△DNE(ASA),
∴FM=EN,
∵AB=AC,BD=CD,
∴AD⊥BC.
∵∠B=∠C=30°,
∴AD=![]() AB=
AB=![]() AC=3,∠BAD=∠CAD=60°.
AC=3,∠BAD=∠CAD=60°.
又∵DM⊥AB,DN⊥AC,
∴∠ADM=∠ADN=30°,
∴AM=AN=![]() AD=
AD=![]() ,
,
∴BM=CN=![]() ,
,
∴BF+CE=BM﹣FM+CN+EN=2BM=9,是定值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
【題目】某文化用品商店用![]() 元采購一批書包,上市后發(fā)現(xiàn)供不應求,很快銷售完了.商店又去采購第二批同樣款式的書包,進貨單價比第一次高
元采購一批書包,上市后發(fā)現(xiàn)供不應求,很快銷售完了.商店又去采購第二批同樣款式的書包,進貨單價比第一次高![]() 元,商店用了
元,商店用了![]() 元,所購數(shù)量是第一次的
元,所購數(shù)量是第一次的![]() 倍.
倍.
(1)求第一批采購的書包的單價是多少元?
(2)若商店按售價為每個書包![]() 元,銷售完這兩批書包,總共獲利多少元?
元,銷售完這兩批書包,總共獲利多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(數(shù)學問題)在同一直角坐標系內直線![]() 與
與![]() ,當
,當![]() 滿足什么條件時,這兩條直線互相垂直?
滿足什么條件時,這兩條直線互相垂直?
探究問題:我們采取一般問題特殊化的策略來進行探究.
探究一:如圖①,在同一直角坐標系內直線![]() 與
與![]() 有怎樣的位置關系?
有怎樣的位置關系?
解:如圖①,設點![]() 在直線
在直線![]() 上,則點
上,則點![]() 一定在直線
一定在直線![]() 上.過點
上.過點![]() 分別作
分別作![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() .
.
則![]() ,
,![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐標系內直線![]() 與
與![]() 互相垂直.
互相垂直.
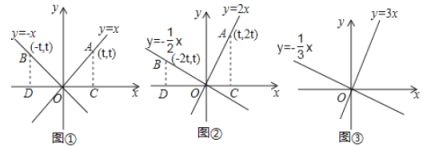
探究二:如圖②,在同一直角坐標系內直線![]() 上,則點
上,則點![]() 一定在直線
一定在直線![]() 上.過點
上.過點![]() 分別作
分別作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐標系內直線![]() 與
與![]() 互相垂直.
互相垂直.
探究三:如圖③,在同一直角坐標系內直線![]() 與
與![]() 有怎樣的位置關系?
有怎樣的位置關系?
(仿照上述方法解答,寫出探究過程)
(1)在同一直角坐標系內直線![]() 與
與![]() ,當
,當![]() 滿足數(shù)量關系為 時,這兩條直線互相垂直.
滿足數(shù)量關系為 時,這兩條直線互相垂直.
(2)在同一直角坐標系內已知直線![]() 與直線
與直線![]() ,使它與直線
,使它與直線![]() 互相垂直,
互相垂直,![]() 的值為: ;兩直線垂足的坐標為: .
的值為: ;兩直線垂足的坐標為: .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商場銷售某種品牌的手機,每部進貨價為2500元.市場調研表明:當銷售價為2900元時,平均每天能售出8部;而當銷售價每降低50元時,平均每天就能多售出4部.
(1)當售價為2800元時,這種手機平均每天的銷售利潤達到多少元?
(2)若設每部手機降低x元,每天的銷售利潤為y元,試寫出y與x之間的函數(shù)關系式.
(3)商場要想獲得最大利潤,每部手機的售價應訂為為多少元?此時的最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
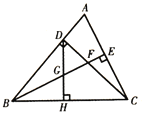
【題目】如圖,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,與
,與![]() 相交于點
相交于點![]() ,
,![]() 是
是![]() 邊的中點,連接
邊的中點,連接![]() 與
與![]() 相交于點
相交于點![]() ,下列結論:
,下列結論:![]() ;
;![]() ;
;![]() ;
;![]() ,其中正確的有__________(填序號).
,其中正確的有__________(填序號).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
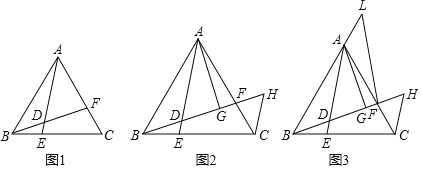
【題目】△ABC是等邊三角形,點E、F分別是邊BC、AC上的點,且BE=CF,AE、BF交于點D.
(1)如圖1,求證:AE=BF.
(2)如圖2,過點A作AG⊥BF于點G,過點C作CH∥AE交BF延長線于點H,若D為BG中點,求BH:CH的值;
(3)如圖3,在(2)的條件下,L為BA延長線上一點,且FL=FB,△FLA的面積為2,求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某測量隊在山腳A處測得山上樹頂仰角為45°(如圖),測量隊在山坡上前進600米到D處,再測得樹頂?shù)难鼋菫?/span>60°,已知這段山坡的坡角為30°,如果樹高為15米,則山高為( )(精確到1米, ![]() =1.732).
=1.732).
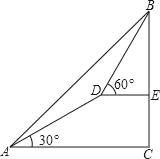
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
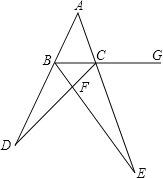
【題目】如圖,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,延長
,延長![]() 至點
至點![]() 平分
平分![]() ,且
,且![]() 的延長線交于點
的延長線交于點![]() ,若
,若![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 求
求![]() 的度數(shù);
的度數(shù);
![]() 若在圖中繼續(xù)作
若在圖中繼續(xù)作![]() 與
與![]() 的平分線交于點
的平分線交于點![]() ,作
,作![]() 與
與![]() 的平分線交于點
的平分線交于點![]() ,作
,作![]() 與
與![]() 的平分線交于點
的平分線交于點![]() ,以此類推,作
,以此類推,作![]() 與
與![]() 的平分線交于點
的平分線交于點![]() ,請用含有
,請用含有![]() 的式了表示
的式了表示![]() 的度數(shù)(直接寫答案).
的度數(shù)(直接寫答案).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小明在學習二次根式后,發(fā)現(xiàn)一些含根號的式子可以寫成另一個式子的平方,如:3+2![]() ,善于思考的小明進行了以下探索:
,善于思考的小明進行了以下探索:
設a+b![]() (其中a、b、m、n均為整數(shù)),
(其中a、b、m、n均為整數(shù)),
則有:a+b![]() ,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b
,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
(1)當a、b、m、n均為正整數(shù)時,若a+b![]() ,用含m、n的式子分別表示a、b得:a= ,b= ;
,用含m、n的式子分別表示a、b得:a= ,b= ;
(2)利用所探索的結論,用完全平方式表示出:7+4![]() = .
= .
(3)請化簡:![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com