
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 內一點,
內一點,![]() ,
,![]() 為
為![]() 延長線上的一點,且
延長線上的一點,且![]() .
.
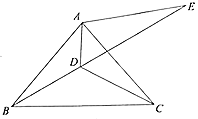
(1)求![]() 的度數;
的度數;
(2)求證:![]() 平分
平分![]() ;
;
(3)請判斷![]() ,
,![]() ,
,![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
【答案】(1)![]() ;(2)見解析;(3)結論:
;(2)見解析;(3)結論:![]() ,見解析.
,見解析.
【解析】
(1)由等腰三角形的性質可得∠ABC=∠ACB,根據角的和差關系可得∠DBC=∠DCB,可得BD=CD,利用SAS可證明△ADB≌△ADC,可得∠BAD=∠CAD,即可求出∠BAD的度數;
(2)利用三角形外角性質可得∠ADE=60°,根據三角形內角和定理可得∠ABC=∠ACB=50°,即可得出![]() =30°,利用外角性質可得∠CDE=60°,即可證明∠ADE=∠CDE,可得
=30°,利用外角性質可得∠CDE=60°,即可證明∠ADE=∠CDE,可得![]() 平分
平分![]() ;
;
(3)在![]() 上取點
上取點![]() ,使
,使![]() ,連接
,連接![]() ,根據等腰三角形的性質可得∠ABE=∠E,由DF=DA,∠ADE=60°可證明△ADF是等邊三角形,可得
,根據等腰三角形的性質可得∠ABE=∠E,由DF=DA,∠ADE=60°可證明△ADF是等邊三角形,可得![]() ,利用AAS可證明
,利用AAS可證明![]() ,可得BD=EF,即可證明
,可得BD=EF,即可證明![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 與
與![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() .
.
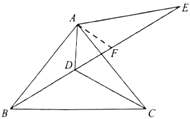
(3)結論:![]() ,
,
在![]() 上取點
上取點![]() ,使
,使![]() ,連接
,連接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 與
與![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,AC是⊙O的直徑,弦BD⊥AO于E,連接BC,過點O作OF⊥BC于F,若BD=8cm,AE=2cm,則OF的長度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
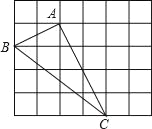
【題目】如圖,在邊長為1的小正方形組成的網格中,△ABC的三個頂點均在格點上,請按要求完成下列各題:
(1)畫線段AD∥BC且使AD=BC,連接CD;
(2)線段AC的長為 ,CD的長為 ,AD的長為_____;
(3)△ACD為 三角形,四邊形ABCD的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
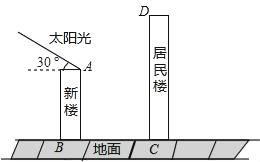
【題目】某住宅小區有一棟面朝正南的居民樓(如圖),該居民樓的一樓高為6米的小區超市,超市以上是居民住房.在該樓的前面15米處要蓋一棟高20米的新樓.已知冬季正午的陽光與水平線的夾角為30°時.
(1)新樓的建造對超市以上的居民住房冬季正午的采光是否有影響,為什么?
(2)若要使超市冬季正午的采光不受影響,新樓應建在相距居民樓至少多少米的地方,為什么?(結果保留整數,參考數據:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市對進貨價為10元/千克的某種蘋果的銷售情況進行統計,發現每天銷售量y(千克)與銷售價x(元/千克)存在一次函數關系,如圖所示.
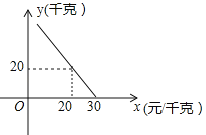
(1)求y關于x的函數關系式(不要求寫出x的取值范圍);
(2)應怎樣確定銷售價,使該品種蘋果的每天銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中(AD>AB),點E是BC上一點,且DE=DA,AF⊥DE,垂足為點F,在下列結論中,不一定正確的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.
x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com