
【題目】觀察分析下列方程:
①![]() 的解是
的解是![]() 或
或![]() ;
;
②![]() 的解是
的解是![]() 或
或![]() ;
;
③![]() 的解是
的解是![]() 或
或![]() ;
;
……
利用它們所蘊含的規律,則關于![]() 的方程
的方程![]() (
(![]() 為正整數)的解是_____.
為正整數)的解是_____.
【答案】x=n+3或x=n+4
【解析】
根據已知三個分式方程和分式方程的解可得出規律:方程左邊分式的分母是方程的解的乘積,方程右邊是方程的解的和,把x-3看成一個整體,根據規律即可得答案.
①中,方程的解為x=1或x=2,1×2=2,1+2=3,
②中,方程的解為x=2或x=3,2×3=6,2+3=5,
③中,方程的解為x=3或x=4,3×4=12,3+4=7,
……
∴關于x的方程x+![]() =2a+1(a為正整數)的解為x=a或x=a+1,
=2a+1(a為正整數)的解為x=a或x=a+1,
把![]() 變形得:
變形得:![]() ,
,
∴x-3=n或x-3=n+1,
∴x=n+3或x=n+4,
∴關于![]() 的方程
的方程![]() (
(![]() 為正整數)的解是x=n+3或x=n+4,
為正整數)的解是x=n+3或x=n+4,
故答案為:x=n+3或x=n+4


科目:初中數學 來源: 題型:
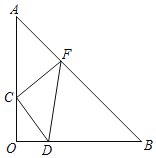
【題目】如圖,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角頂點C在邊OA上,點D在邊OB上,點F在邊AB上,如果△CDF的面積是△AOB的面積的![]() ,OD=2,則△AOB的面積為____.
,OD=2,則△AOB的面積為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某工程隊準備在山坡(山坡視為直線l)上修一條路,需要測量山坡的坡度,即tanα的值.測量員在山坡P處(不計此人身高)觀察對面山頂上的一座鐵塔,測得塔尖C的仰角為31°,塔底B的仰角為26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,圖中的點O、B、C、A、P在同一平面內.
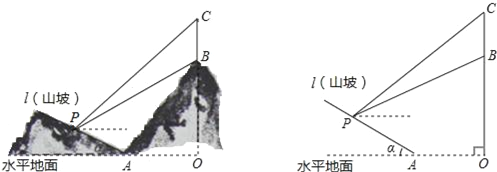
求:
(1)P到OC的距離.
(2)山坡的坡度tanα.
(參考數據sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,以
,以![]() 的一邊為邊畫等腰三角形,使得它的第三個頂點在
的一邊為邊畫等腰三角形,使得它的第三個頂點在![]() 的其他邊上,則可以畫出的不同的等腰三角形的個數最多可畫幾個?( )
的其他邊上,則可以畫出的不同的等腰三角形的個數最多可畫幾個?( )
A.9個B.7個C.6個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古埃及人用下面的方法得到直角三角形,把一根長繩打上等距離的13個結(12段),然后用樁釘釘成一個三角形,如圖1,其中∠C便是直角.
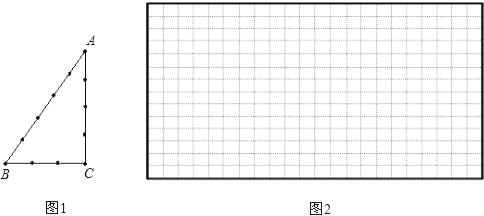
(1)請你選擇古埃及人得到直角三角形這種方法的理由 (填A或B)
A.勾股定理:在直角三角形邊的兩直角邊的平方和等于斜邊的平方
B.勾股定理逆定理:如果三角形的三邊長a、b、c有關系:a2+b2=c2,那么這個三角形是直角三角形
(2)如果三個正整數a、b、c滿足a2+b2=c2,那么我們就稱 a、b、c是一組勾股數,請你寫出一組勾股數
(3)仿照上面的方法,再結合上面你寫出的勾股數,你能否只用繩子,設計一種不同于上面的方法得到一個直角三角形(在圖2中,只需畫出示意圖.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,點O在AB上,經過點A的⊙O與BC相切于點D,交AB于點E.
(1)求證:AD平分∠BAC;
(2)若CD=1,求圖中陰影部分的面積(結果保留π).
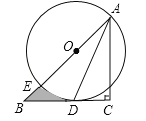
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,D在邊AC上,且
,D在邊AC上,且![]() .
.
![]() 如圖1,填空
如圖1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如圖2,若M為線段AC上的點,過M作直線
如圖2,若M為線段AC上的點,過M作直線![]() 于H,分別交直線AB、BC與點N、E.
于H,分別交直線AB、BC與點N、E.
![]() 求證:
求證:![]() 是等腰三角形;
是等腰三角形;
![]() 試寫出線段AN、CE、CD之間的數量關系,并加以證明.
試寫出線段AN、CE、CD之間的數量關系,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司需招聘一名員工,對應聘者甲、乙、丙從筆試、面試、體能三個方面進行量化考核.甲、乙、丙各項得分如下表:
筆 試 | 面 試 | 體 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根據三項得分的平均分,從高到低確定三名應聘者的排名順序.
(2)該公司規定:筆試,面試、體能得分分別不得低于80分,80分,70分,并按60%,30%,10%的比例計入總分(不計其他因素條件),請你說明誰將被錄用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
為了響應“十三五”規劃中提出的綠色環保的倡議,某校文印室提出了每個人都踐行“雙面打印,節約用紙”.已知打印一份資料,如果用A4厚型紙單面打印,總質量為400克,將其全部改成雙面打印,用紙將減少一半;如果用A4薄型紙雙面打印,這份資料的總質量為160克,已知每頁薄型紙比厚型紙輕0.8克,求A4薄型紙每頁的質量.(墨的質量忽略不計)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com