Question

如圖，已知AB∥CD，則∠B、∠E、∠D三角的關系．

Answer 1

答案：
解析：

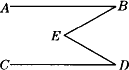
[探究過程]觀察圖形比較∠B、∠D、∠E的角的大小關系，易見∠E＞∠B，∠E＞∠D，用量角器可以具體度量其大小，比較還易發現∠E＝∠B＋∠D的關系，重新畫幾幅類似的圖，再度量比較是否仍具有∠E＝∠B＋∠D的關系？始終發現有如此關系．因此可猜想∠E＝∠B＋∠D關系，再通過理論依據進行邏輯推理去驗證．如下：過點E作EF∥AB，則∠B＝∠BEF，又∵AB∥CD，∴EF∥CD，∴∠DEF＝∠D，故∠BEF＋∠DEF＝∠B＋∠D，即∠BED＝∠B＋∠D．或用第二種證法：連結BD，∵AB∥CD，∴∠ABD＋∠CDB＝180°，即∠ABE＋∠EBC＋∠CDE＋∠BDE＝180°．又∵∠E＋∠BCE＋∠CBE＝180°，∴∠E＝∠ABE＋∠CDE．或證法三：延長BE交CD于點F，∵AB∥CD，∴∠B＝∠EFD．∵∠EFD＋∠D＋∠DEF＝180°，∠DEF＋∠BED＝180°，∴∠BED＝∠EFD＋∠D＝∠B＋∠D． 　　[探究評析]本題通過畫多種類似圖形來探索∠B、∠D、∠E的關系，然后通過添加不同的輔助線來證明．在論題中畫輔助線起了鋪路搭橋的作用，化難為易，不同的輔助線導致了不同的方法，充分展示了幾何的靈活多樣性．