
【題目】如圖,在平面直角坐標(biāo)系中,OA⊥OB,AB⊥x軸于點(diǎn)C,點(diǎn)A( ![]() ,1)在反比例函數(shù)y=
,1)在反比例函數(shù)y= ![]() 的圖象上.
的圖象上.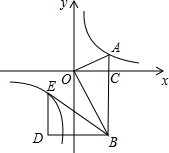
(1)求反比例函數(shù)y= ![]() 的表達(dá)式;
的表達(dá)式;
(2)在x軸的負(fù)半軸上存在一點(diǎn)P,使得S△AOP= ![]() S△AOB , 求點(diǎn)P的坐標(biāo);
S△AOB , 求點(diǎn)P的坐標(biāo);
(3)若將△BOA繞點(diǎn)B按逆時(shí)針?lè)较蛐D(zhuǎn)60°得到△BDE.直接寫(xiě)出點(diǎn)E的坐標(biāo),并判斷點(diǎn)E是否在該反比例函數(shù)的圖象上.
【答案】
(1)
解:∵點(diǎn)A( ![]() ,1)在反比例函數(shù)y=
,1)在反比例函數(shù)y= ![]() 的圖象上,
的圖象上,
∴k= ![]() ×1=
×1= ![]() ,
,
∴反比例函數(shù)表達(dá)式為y= ![]() .
.
(2)
解:∵A( ![]() ,1),AB⊥x軸于點(diǎn)C,
,1),AB⊥x軸于點(diǎn)C,
∴OC= ![]() ,AC=1,
,AC=1,
∵OA⊥OB,OC⊥AB,
∴∠A=∠COB,
∴tan∠A= ![]() =tan∠COB=
=tan∠COB= ![]() ,
,
∴OC2=ACBC,即BC=3,
∴AB=4,
∴S△AOB= ![]() ×
× ![]() ×4=2
×4=2 ![]() ,
,
∴S△AOP= ![]() S△AOB=
S△AOB= ![]() ,
,
設(shè)點(diǎn)P的坐標(biāo)為(m,0),
∴ ![]() ×|m|×1=
×|m|×1= ![]() ,解得|m|=2
,解得|m|=2 ![]() ,
,
∵P是x軸的負(fù)半軸上的點(diǎn),
∴m=﹣2 ![]() ,
,
∴點(diǎn)P的坐標(biāo)為(﹣2 ![]() ,0)
,0)
(3)
解:由(2)可知tan∠COB= ![]() =
= ![]() =
= ![]() ,
,
∴∠COB=60°,
∴∠ABO=30°,
∵將△BOA繞點(diǎn)B按逆時(shí)針?lè)较蛐D(zhuǎn)60°得到△BDE,
∴∠OBD=60°,
∴∠ABD=90°,
∴BD∥x軸,
在Rt△AOB中,AB=4,∠ABO=30°,
∴AO=DE=2,OB=DB=2 ![]() ,且BC=3,OC=
,且BC=3,OC= ![]() ,
,
∴OD=DB﹣OC= ![]() ,BC﹣DE=1,
,BC﹣DE=1,
∴E(﹣ ![]() ,﹣1),
,﹣1),
∵﹣ ![]() ×(﹣1)=
×(﹣1)= ![]() ,
,
∴點(diǎn)E在該反比例函數(shù)圖象上
【解析】(1)由點(diǎn)A的坐標(biāo),利用待定系數(shù)法可求得反比例函數(shù)表達(dá)式;(2)由條件可求得∠A=∠COB,利用三角函數(shù)的定義可得到OC2=ACBC,可求得BC的長(zhǎng),可求得△AOB的面積,設(shè)P點(diǎn)坐標(biāo)為(m,0),由題意可得到關(guān)于m的方程,可求得m的值;(3)由條件可求得∠ABD=90°,則BD∥x軸,由BD、DE的長(zhǎng),可求得E點(diǎn)坐標(biāo),代入反比例函數(shù)解析式進(jìn)行判斷即可.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,與∠1是同位角的是__________,與∠1是內(nèi)錯(cuò)角的是__________,與∠1是同旁?xún)?nèi)角的是__________.
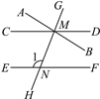
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知一次函數(shù)![]() 的圖像與
的圖像與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,一次函數(shù)
,一次函數(shù)![]() 的圖像過(guò)點(diǎn)
的圖像過(guò)點(diǎn)![]() ,且與
,且與![]() 軸及
軸及![]() 的圖像分別交于點(diǎn)
的圖像分別交于點(diǎn)![]() 、
、![]() ,
,![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() .
.
(1)求n的值及一次函數(shù)![]() 的解析式.
的解析式.
(2)求四邊形![]() 的面積.
的面積.
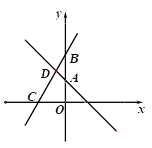
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=60°,AB=2,點(diǎn)P是這個(gè)菱形內(nèi)部或邊上的一點(diǎn),若以點(diǎn)P、B、C為頂點(diǎn)的三角形是等腰三角形,則P、D(P、D兩點(diǎn)不重合)兩點(diǎn)間的最短距離為 . 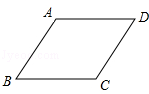
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)O是△ABC內(nèi)一點(diǎn),連結(jié)OB、OC,并將AB、OB、OC、AC的中點(diǎn)D、E、F、G依次連結(jié),得到四邊形DEFG. 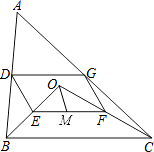
(1)求證:四邊形DEFG是平行四邊形;
(2)若M為EF的中點(diǎn),OM=3,∠OBC和∠OCB互余,求DG的長(zhǎng)度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,兩個(gè)反比例函數(shù)y1= ![]() (其中k1>0)和y2=
(其中k1>0)和y2= ![]() 在第一象限內(nèi)的圖象依次是C1和C2 , 點(diǎn)P在C1上.矩形PCOD交C2于A、B兩點(diǎn),OA的延長(zhǎng)線交C1于點(diǎn)E,EF⊥x軸于F點(diǎn),且圖中四邊形BOAP的面積為6,則EF:AC為( )
在第一象限內(nèi)的圖象依次是C1和C2 , 點(diǎn)P在C1上.矩形PCOD交C2于A、B兩點(diǎn),OA的延長(zhǎng)線交C1于點(diǎn)E,EF⊥x軸于F點(diǎn),且圖中四邊形BOAP的面積為6,則EF:AC為( ) 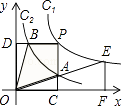
A.![]() ﹕1
﹕1
B.2﹕ ![]()
C.2﹕1
D.29﹕14
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】?jī)山M鄰邊分別相等的四邊形叫做“箏形”,如圖,四邊形ABCD是一個(gè)箏形,其中AD=CD,AB=CB,在探究箏形的性質(zhì)時(shí),得到如下結(jié)論:①△ABD≌△CBD;②AC⊥BD;③四邊形ABCD的面積= ![]() ACBD,其中正確的結(jié)論有( )
ACBD,其中正確的結(jié)論有( ) 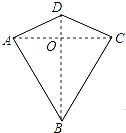
A.0個(gè)
B.1個(gè)
C.2個(gè)
D.3個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
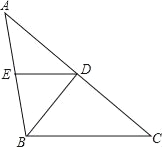
【題目】如圖,在△ABC中,AB=BC,∠ABC=100°,BD是∠ABC的平分線,E是AB的中點(diǎn).
(1)證明DE∥BC;(2)求∠EDB的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直線AB、CD相交于點(diǎn)O,下列條件中,不能說(shuō)明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com