
【題目】如圖,直線![]() 的解析表達式為
的解析表達式為![]() ,且
,且![]() 與
與![]() 軸交于點
軸交于點![]() .直線
.直線![]() 經過點
經過點![]() 、
、![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求直線![]() 的解析表達式;
的解析表達式;
(3)求![]() 的面積;
的面積;
(4)在直線![]() 上存在異于點
上存在異于點![]() 的另一個點
的另一個點![]() ,使得
,使得![]() 與
與![]() 的面積相等,求
的面積相等,求![]() 點的坐標.
點的坐標.
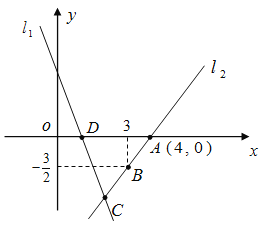
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)P點坐標為(6,3).
;(4)P點坐標為(6,3).
【解析】試題分析:(1)因為點D是一次函數![]() 與x軸的交點,所以令y=0,即可求出點D坐標,
與x軸的交點,所以令y=0,即可求出點D坐標,
(2)設直線![]() 的解析式為:
的解析式為:![]() ,將點A,B坐標代入列二元一次方程組即可求出k,b,即可得
,將點A,B坐標代入列二元一次方程組即可求出k,b,即可得![]() 的解析式,
的解析式,
(3)因為點C是直線![]() 和直線
和直線![]() 的交點,可將兩直線所在解析式聯立方程組,求出點C坐標,再根據點A,D可得三角形的底邊長,由點C的縱坐標可得三角形的高,代入三角形面積公式進行計算即可求解,
的交點,可將兩直線所在解析式聯立方程組,求出點C坐標,再根據點A,D可得三角形的底邊長,由點C的縱坐標可得三角形的高,代入三角形面積公式進行計算即可求解,
(4)根據△![]() 與△
與△![]() 的面積相等,可知點P與點C到x軸的距離相等,且又不同于點C,所以求出點P的縱坐標,然后代入直線
的面積相等,可知點P與點C到x軸的距離相等,且又不同于點C,所以求出點P的縱坐標,然后代入直線![]() 的解析式即可求解.
的解析式即可求解.
試題解析:(1)∵ y=﹣3x+3,
∴令y=0,得﹣3x+3=0,解得x=1,
∴D(1,0),
(2)設直線l2的解析表達式為y=kx+b,由圖象知:x=4,y=0,x=3,y=![]() ,代入表達式y=kx+b,得
,代入表達式y=kx+b,得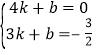 ,解得
,解得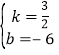 ,所以直線l2的解析表達式為y=
,所以直線l2的解析表達式為y=![]() ,
,
(3)由圖象可得: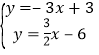 ,解得
,解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ,
,
(4)因為點P與點C到AD的距離相等,所以P點的縱坐標為3,當y=3時,![]() ,解得x=6,所以P點坐標為(6,3).
,解得x=6,所以P點坐標為(6,3).


科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,沿EF將矩形折疊,使A、C重合,AC與EF交于點H.
(1)求證:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】柯橋區某企業因為發展需要,從外地調運來一批94噸的原材料,現有甲、乙、丙三種車型共選擇,每輛車的運載能力和運費如下表所示:(假設每輛車均滿載)
車型 | 甲 | 乙 | 丙 |
汽車運載量(噸/輛) | 5 | 8 | 10 |
汽車運費(元/輛) | 400 | 500 | 600 |
(1)若全部物資都用甲、乙兩種車型來運送,需運費6400元,問分別需甲、乙兩種車型各幾輛?
(2)為了節省運費,該地政府打算用甲、乙、丙三種車型同時參與運送,已知它們的總輛數為14輛,你能分別求出三種車型的輛數嗎?此時的運費又是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線![]() 可變形為:
可變形為:![]() ,則點P(
,則點P(![]() )到直線
)到直線![]() 的距離d可用公式
的距離d可用公式![]() 計算.
計算.
例如:求點P(-2,1)到直線![]() 的距離.
的距離.
解:因為直線![]() 可變形為
可變形為![]() ,其中
,其中![]() ,
,![]() .
.
所以點P(-2,1)到直線![]() 的距離為
的距離為![]() .
.
根據以上材料求:
(1)點P(2,-1)到直線![]() 的距離;
的距離;
(2)已知M為直線![]() 上的點,且M到直線
上的點,且M到直線![]() 的距離為
的距離為![]() ,求M的坐標;
,求M的坐標;
(3)已知線段![]() 上的點到直線
上的點到直線![]() 的最小距離為1,求k的值.
的最小距離為1,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E是AD上的一個動點,連接BE,作點A關于BE的對稱點F,且點F落在矩形ABCD的內部,連結AF,BF,EF,過點F作GF⊥AF交AD于點G,設 ![]() =n.
=n.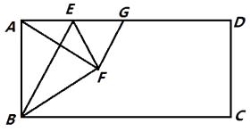
(1)求證:AE=GE;
(2)當點F落在AC上時,用含n的代數式表示 ![]() 的值;
的值;
(3)若AD=4AB,且以點F,C,G為頂點的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按如下方法,將△ABC的三邊縮小的原來的![]() ,如圖,任取一點O,連AO、BO、CO,并取它們的中點D、E、F,得△DEF,則下列說法正確的是( )
,如圖,任取一點O,連AO、BO、CO,并取它們的中點D、E、F,得△DEF,則下列說法正確的是( )
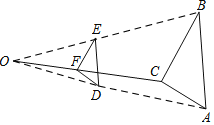
A. △ABC與△DEF不是位似圖形 B. ![]() =
=![]()
C. △ABC與△DEF的周長比為1:2 D. △ABC與△DEF的面積比為4:1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮企業生產部有技術工人15人,生產部為了合理制定產品的每月生產定額,統計了15人某月的加工零件個數:
每人加工件數 | 540 | 450 | 300 | 240 | 210 | 120 |
人數 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)寫出這15人該月加工零件數的平均數、中位數和眾數。
(2)若以本次統計所得的月加工零件數的平均數定為每位工人每月的生產定額,你認為這個定額是否合理,為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com