
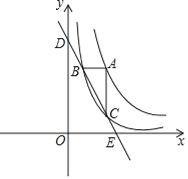
【題目】如圖,點(diǎn)A在函數(shù)y=![]() (x>0)圖象上,過(guò)點(diǎn)A作x軸和y軸的平行線分別交函數(shù)y=
(x>0)圖象上,過(guò)點(diǎn)A作x軸和y軸的平行線分別交函數(shù)y=![]() 圖象于點(diǎn)B,C,直線BC與坐標(biāo)軸的交點(diǎn)為D,E.
圖象于點(diǎn)B,C,直線BC與坐標(biāo)軸的交點(diǎn)為D,E.
(1)當(dāng)點(diǎn)C的橫坐標(biāo)為1時(shí),求點(diǎn)B的坐標(biāo);
(2)試問(wèn):當(dāng)點(diǎn)A在函數(shù)y=![]() (x>0)圖象上運(yùn)動(dòng)時(shí),△ABC的面積是否發(fā)生變化?若不變,請(qǐng)求出△ABC的面積,若變化,請(qǐng)說(shuō)明理由.
(x>0)圖象上運(yùn)動(dòng)時(shí),△ABC的面積是否發(fā)生變化?若不變,請(qǐng)求出△ABC的面積,若變化,請(qǐng)說(shuō)明理由.
(3)試說(shuō)明:當(dāng)點(diǎn)A在函數(shù)y=![]() (x>0)圖象上運(yùn)動(dòng)時(shí),線段BD與CE的長(zhǎng)始終相等.
(x>0)圖象上運(yùn)動(dòng)時(shí),線段BD與CE的長(zhǎng)始終相等.
【答案】(1)B點(diǎn)坐標(biāo)為(![]() ,4);
,4);
(2)即△ABC的面積不發(fā)生變化,其面積為![]() ;
;
(3)證明見(jiàn)解析.
【解析】試題分析:(1)由條件可先求得A點(diǎn)坐標(biāo),從而可求得B點(diǎn)縱坐標(biāo),再代入y=![]() 可求得B點(diǎn)坐標(biāo);
可求得B點(diǎn)坐標(biāo);
(2)可設(shè)出A點(diǎn)坐標(biāo),從而可表示出C、B的坐標(biāo),則可表示出AB和AC的長(zhǎng),可求得△ABC的面積;
(3)可證明△ABC∽△EFC,利用(2)中,AB和AC的長(zhǎng)可表示出EF,可得到BG=EF,從而可證明△DBG≌△CFE,可得到DB=CF.
解析:(1)∵點(diǎn)C在y=![]() 的圖象上,且C點(diǎn)橫坐標(biāo)為1,
的圖象上,且C點(diǎn)橫坐標(biāo)為1,
∴C(1,1),
∵AC∥y軸,AB∥x軸,
∴A點(diǎn)橫坐標(biāo)為1,
∵A點(diǎn)在函數(shù)y=![]() (x>0)圖象上,
(x>0)圖象上,
∴A(1,4),
∴B點(diǎn)縱坐標(biāo)為4,
∵點(diǎn)B在y=![]() 的圖象上,
的圖象上,
∴B點(diǎn)坐標(biāo)為(![]() ,4);
,4);
(2)設(shè)A(a,![]() ),則C(a,
),則C(a,![]() ),B(
),B(![]() ,
,![]() ),
),
∴AB=a﹣![]() =
=![]() a,AC=
a,AC=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△ABC=![]() ABAC=
ABAC=![]() ,
,
即△ABC的面積不發(fā)生變化,其面積為![]() ;
;
(3)如圖,設(shè)AB的延長(zhǎng)線交y軸于點(diǎn)G,AC的延長(zhǎng)線交x軸于點(diǎn)F,
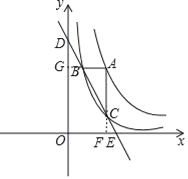
∵AB∥x軸,
∴△ABC∽△EFC,
∴![]() ,即
,即![]() ,
,
∴EF=![]() a,
a,
由(2)可知BG=![]() a,
a,
∴BG=EF,
∵AE∥y軸,∴∠BDG=∠FCE,
在△DBG和△CFE中
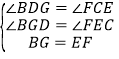
∴△DBG≌△CEF(AAS),
∴BD=EF.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】同時(shí)拋擲A,B兩個(gè)均勻的小立方體(每個(gè)面上分別標(biāo)有數(shù)字1,2,3,4,5,6),設(shè)兩立方體朝上的數(shù)字分別為x,y,并以此確定點(diǎn)P(x,y),那么點(diǎn)P落在直線y=-2x+9上的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 為
為![]() 的高,
的高,![]() 為
為![]() 的角平分線,若
的角平分線,若![]() ,
,![]() .
.

(1)![]() ;
;
(2)求![]() 的度數(shù);
的度數(shù);
(3)若點(diǎn)![]() 為線段
為線段![]() 上任意一點(diǎn),當(dāng)
上任意一點(diǎn),當(dāng)![]() 為直角三角形時(shí),則求
為直角三角形時(shí),則求![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】一塊直角三角形木板,它的一條直角邊AB長(zhǎng)1.5m,面積為1.5m2.甲、乙兩位木匠分別按圖①、②把它加工成一個(gè)正方形桌面.請(qǐng)說(shuō)明哪個(gè)正方形面積較大(加工損耗不計(jì)).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() ,將
,將![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)
順時(shí)針旋轉(zhuǎn)![]() 至
至![]() ,點(diǎn)
,點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)分別是
的對(duì)應(yīng)點(diǎn)分別是![]() ,連接
,連接![]() 線段
線段![]() 與線段
與線段![]() 交于點(diǎn)M,連接
交于點(diǎn)M,連接![]() .
.
(1)如圖1,求證:![]() ;
;
(2)如圖1,求證:OM平分![]() ;
;
(3)如圖2,若![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).


查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,一輛汽車(chē)和一輛摩托車(chē)分別從A,B兩地去同一城市,l1 ,l2分別表示汽車(chē)、摩托車(chē)離A地的距離s(km)隨時(shí)間t(h)變化的圖象,則下列結(jié)論:①摩托車(chē)比汽車(chē)晚到1 h;②A,B兩地的距離為20 km;③摩托車(chē)的速度為45 km/h,汽車(chē)的速度為60 km/h;④汽車(chē)出發(fā)1 h后與摩托車(chē)相遇,此時(shí)距離B地40 km;⑤相遇前摩托車(chē)的速度比汽車(chē)的速度快.其中正確的結(jié)論有( )

A. 2個(gè) B. 3個(gè) C. 4個(gè) D. 5個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,兩根長(zhǎng)度為12米的繩子,一端系在旗桿上的同一位置A點(diǎn),另一端分別固定在地面上的兩個(gè)木樁B,C上(繩結(jié)處的誤差忽略不計(jì)),現(xiàn)在只有一把卷尺,如何檢驗(yàn)旗桿是否垂直于地面BC?請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
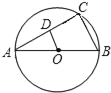
【題目】如圖,已知AB為⊙O的直徑,AC為弦,OD∥BC,交AC于D,BC=4cm.
(1)求證:AC⊥OD;
(2)求OD的長(zhǎng);
(3)若2sinA﹣1=0,求⊙O的直徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
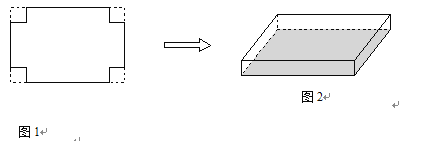
【題目】(本題滿分8分)一張長(zhǎng)為30cm,寬20cm的矩形紙片,如圖1所示,將這張紙片的四個(gè)角各剪去一個(gè)邊長(zhǎng)相同的正方形后,把剩余部分折成一個(gè)無(wú)蓋的長(zhǎng)方體紙盒,如圖1所示,如果折成的長(zhǎng)方體紙盒的底面積為264cm2,求剪掉的正方形紙片的邊長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com